贝叶斯模型Bayesian Model

Posted on Jul 31, 2020 By Jason Hao

宏观理解

为什么贝叶斯模型在各种领域里地位很重要？

  1. 因为LDA模型在主题模型里面起到非常重要的作用。LDA模型是无监督学习模型，可以当作是Mix-membership models的一种，作用是如果给定一篇文章属于多个主题，它可以生成每个主题的概率 分布，而如果用朴素贝叶斯则只能生成一个主题类的预测，也可以叫做Uni-membership model。

  2. 用于小数据量的学习问题。因为小数据量很容易造成过拟合，那解决的方法可以是集成模型，而贝叶斯模型本身也是一个集成模型。而和传统集成模型比如随机森林集成有限个模型不同的是，它集成的是无限多个模型。 但是在数据量比较大的时候贝叶斯模型学起来会很慢。

  3. 把不确定性融合在模型本身。

  4. 把先验融合到模型中。

  5. 模型压缩。

微观分析

贝叶斯是一个很大的领域，所以我们按以下的顺序进行剖析：

  1. 什么是贝叶斯？

  2. 贝叶斯的推理
    2.1 MCMC采样

    2.2 变分法variational inference

  3. xxx

1. 什么是贝叶斯？

说到什么是贝叶斯，我们就要理清楚MLE、MAP和Bayesian的区别。这三个都是构造目标函数的方法，当一个模型分别用这三种方式构造时，形成的模型也是不同的：

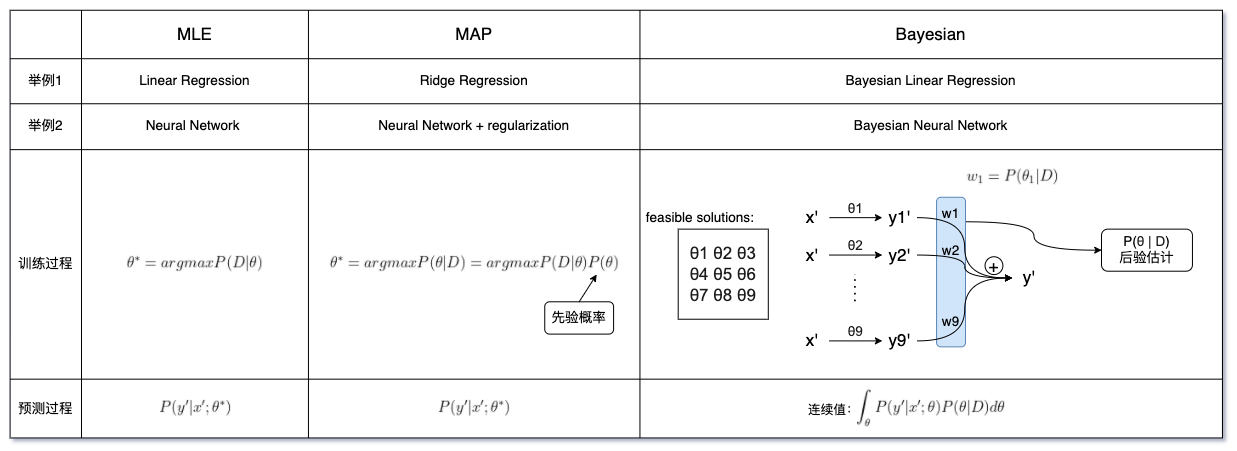
首先最简单的MLE，我们在训练的时候是想求出一个最好的参数Θ，然后使用这个Θ来做预测；MAP和MLE很相似，不一样的是MAP可以理解为加了正则项后的MLE，也可以理解为多了一个先验的MLE，这个先验也会影响最后学出来的Θ值；最后这个Bayesian有些不同，如果说MLE和MAP只是从所有可能取值的Θ中找出最佳的一个Θ，那么贝叶斯做的事情就像是集成模型，不抛弃任何一个Θ，反而让所有的Θ都用来预测最终结果。例如上图中的训练过程，我们会给每一个预测加一个权重，然后学习这个权重。预测过程也是这个套路，首先我们要P(Θ D)估计一下参数分布，然后在某一个特定的参数下乘以前面的部分就是它的期望，如果是连续的我们就求积分，如果是离散的我们就做加法。

2. 贝叶斯的推理

我们上一步已经得到了一个预测过程的公式，可以看出来我们主要要解决的就是后验概率估计P(Θ｜D)，我们不妨先用贝叶斯公式列出来看看：

但是最后这个分母没有办法计算啊。那既然没有办法得到一个确切的值，估计一个差不多的也可以。这就是贝叶斯的approximate inference。

2.1 MCMC采样和变分法

既然积分的计算是无穷的，那么我们可以直接随机采样让它变成有限的，这样问题就解决了。这个随机采样算法我们可以用蒙特卡洛Monte Carlo采样算法。可如果是随机采样，我们无法保证最终的答案趋向于最优解，因为我们很有可能采样了很多很差的可行解，那么怎么处理这个问题呢？Markov Chain Monte Carlo简称MCMC算法可以帮到我们。它不再是随机采样，而是首先找出比较优的一个可行解，然后在这个解的周围寻找下一个可行解。因为它有一个概念基础就是，一个优秀的人周围更大可能存在同样优秀的人。所以按照这个思路，我们采样的n个可行解可以比随机抽样更加趋向于最优解。

除了积分是无穷的我们可以强制采样让它变成有限的以外，还有另一种也很直接的方法就是我们把积分转化成一个更简单的形式，使这个更简单的形式的解无限接近此时的积分，这个叫做变分法variational inference。

3. LDA模型

LDA主题模型用来生成一堆文本的主题分布doc-topic distribution，我们用Θ表示这个分布，例如有3个主题军事、金融、科技，通过LDA会给每个文本生成一个分布向量，【0.1 0.6 0.3】代表每个主题的概率。这个向量也可以当作是文本的表示来计算相似度。 除了这个文本主题分布，LDA还有另外一个输出，是每个单词在主题中的分布topic-word distribution，我们用ϕ表示这个分布。这个结果是一个（v,k）的矩阵，v表示词袋里单词的个数，k表示有多少个主题。表示每个词在每个主题的分布，当然每一列都是和为1的。

Generative process of LDA

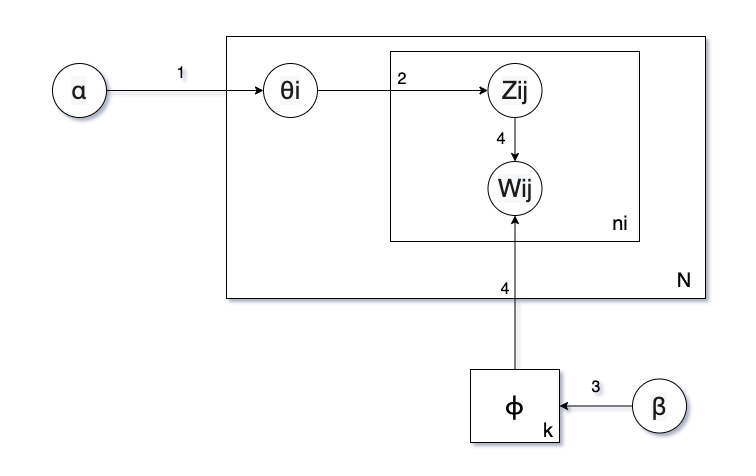
在我们有了这些分布之后，就可以用LDA进行生成文本了。在概率图模型中我们用方框来表示一个loop，下图中最大的方框右下角的N代表这个方框里的东西要循环N次。里面的小方框表示我们的每一个单词循环过程，一共循环生成ni个单词。

第一步：我们要确定一个主题，但是我们不知道当前文本主题应该是哪个，所以我们需要一个先验α来帮助我们生成当前第i个文本的主题分布Θi。
第二步：有了主题分布之后，我们就要生成每一个单词了。但是在生成单词之前我们要抽取每个单词的主题Zij，Zij表示第i个文章里的第j个单词的主题。
第三步：同样的，我们用另一个先验β来生成单词的主题分布ϕ。
第四步：有了每个单词的主题分布ϕ，又有了我们当前抽取的主题Zij，就可以抽取一个单词Wij。
第五步：循环1-4步直到我们生成了该文本需要的ni个单词。

好了，现在我们知道了整体流程了，下一步就是深究一下每一步的细节了。我们说过图中的每一个箭头其实都是一个从分布中sample的过程。那么第一步我们是怎么sample的呢？

第一步

从α我们生成出每篇文章的主题分布Θi，这个Θi我们要满足两个条件：1. 所有的主题的概率加和为1。 2. 每一个主题的概率都要大于0。那么根据这两个条件，我们可以使用Dirichlet（狄利克雷）分布。

也就是说我们Θi是由dirichlet分布和它的参数α采样出来的。

第二步

通过第一步我们可以确定Θi的分布是和为1的，比如我们有四个主题和它们的分布（0.5 0.3 0.1 0.1），那么我们如何从中生成Zij呢？我们可以用Multinomial分布：

第三步

利用β来生成ϕ。我们先想一下ϕ的特点：它是每个词在k个主题上的分布情况，那么就是说ϕ一共应该有｜词库｜的大小。和Θi类似，每个单词上k个主题的概率加和为1并且每一个主题的概率都要大于0。那么我们就可以同样使用Dirichlet（狄利克雷）分布：

第四步

我们有了单词的主题分布ϕ和我们sample的一个单词主题Zij，就可以生成一个单词Wij。那么怎么选择Wij呢？这不是和之前第二步选择主题一样么，同样我们可以用Multinomial分布：

现在我们已经可以按照步骤写出它的后验概率，那么怎么求解呢？这就回到了我们之前提到过的MCMC。

3.1 LDA模型之Gibbs sampling

Gibbs sampling是MCMC中的一种方法，它的步骤和坐标下降法很像，坐标下降法是在学习一个参数的时候固定其他的参数，而吉布斯采样是在采样一个变量的时候固定其他的变量。比如我们要sample一个Θi，我们就要固定其余的所有变量，包括除了Θi以外的所有Θ。

根据markov blanket我们可以找出里面不会影响到Θi的一些项。

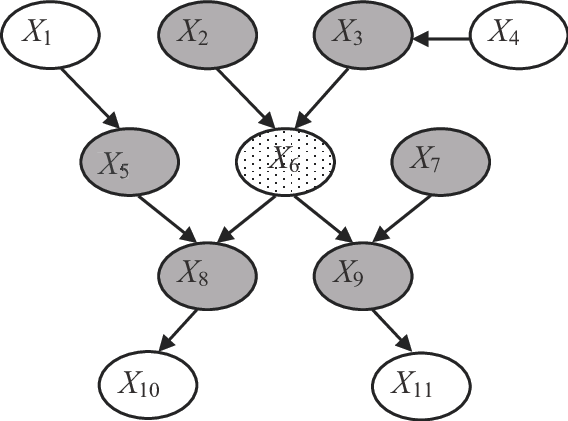
markov blanket指的是在一个概率图中（如上图），我们只认为某些点和x6是造成影响的而非所有。同理我们可以找出Θi的上下游变量，得到：

然后根据Dirichlet的PDF可以推出来其实后验也是遵从Dirichlet分布。这个就是共轭分布，所以在概率图中当我们的先验属于一种分布时我们通常会使它的likelihood为一种形式来产生共轭分布。对于其余的参数求解方式也是一样的。