宏观理解

图神经网络本来被应用在推荐系统、社交网络、知识图谱等，后来人们发现它还可以很好的应用的很多别的领域，所以近期这个领域大火。图神经网络顾名思义其实就是可以在图输入时用到的神经网络架构。比如典型应用有节点分类。说到图神经网络肯定会想到CNN，但是他们的区别是图神经网络可以处理节点不固定的情况。

微观分析

首先我们定义一下图的概念。我们有一个set的节点，一个set的边。如下图所示我们用Xv来表示第v个节点上的特征；用X(v,u)来表示节点v和节点u之间的边上的特征；用hv来表示第v个节点的隐表示。这个隐表示不仅 可以很好的表示它自己，还可以加入和它相连的其他节点的信息。我们的目的就是建立一个这样的结构然后可以求的所有节点的隐表示。那么怎么做呢？

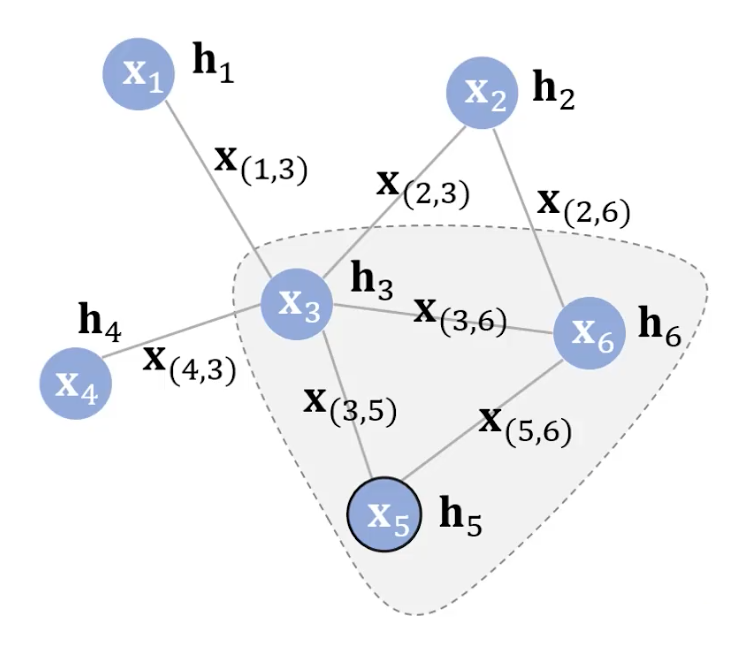
原论文中提到的一种方式是通过迭代的方式：

第一项表示当前节点的特征
第二项表示与当前节点相连接的边的特征
第三项表示当前节点的所有邻居节点的隐表示
第四项表示当前节点的所有邻居节点的特征

例如如果当前节点是x5的话，那么

那么很显而易见的是函数f处理的输入应该是变长的，因为我们根本无法确定有多少邻居和邻边。但是变长的输入总是很困难而且复杂的，我们为了使它变成定长，可以应用一下pooling，无论是多少输入，我都给你avg pooling到 一个固定的维度。

那么这个隐表示一定可以收敛吗？根据巴拿赫不动点定理，答案是肯定的。在定义f的时候会引入一个正则项，来保证每一个节点都可以收敛。

之后我们可以得到每个节点收敛的隐表示。就和语言模型预训练一样，我们可以直接在最后接一个下游任务。比如我们在做一个节点分类，看看微博账号里面哪些账号是僵尸号。在得到隐表示后我们定义一下分类网络g(hv, xv)， 接收当前节点的隐表示和特征，得出一个分类结果。如果是训练过程就在里面加一个loss，再通过反向传播来训练它。

（这里的T是迭代的步数，和时间其实没什么关系）

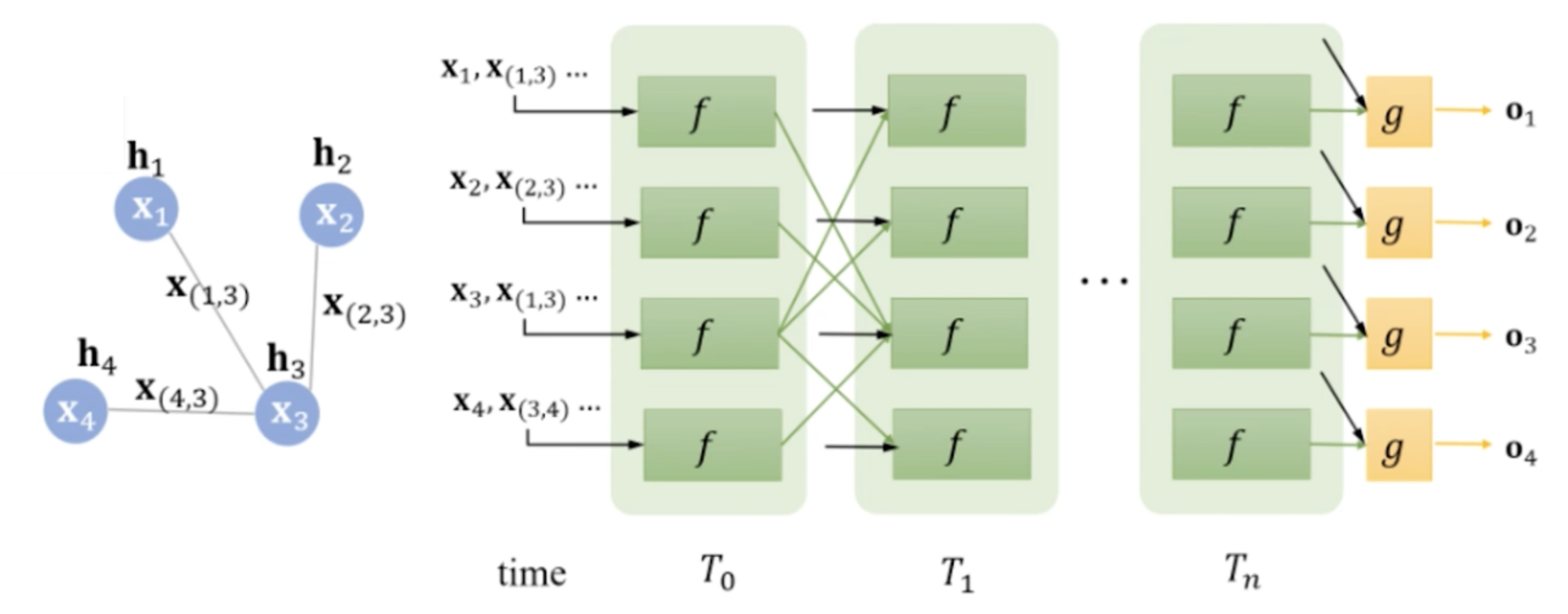
CNN的进化版是加了各种的gate，就好像LSTM一样。同样我们也可以把gate加在GNN里面，叫Gated GNN。他的迭代函数是这样的：

可以发现之前我们有每个节点的特征作为输入，但是GGNN里面却没有，是因为在GGNN中我们用每个节点的特征来初始化了h。再通过和当前节点连接的所有邻居节点和边的权值做一个加权平均，最后过一个GRU。

GCN

对于GNN的研究现在主要是落在了图卷积神经网络上。主旨就是想多叠加一些卷积层来得到更好的隐表示。

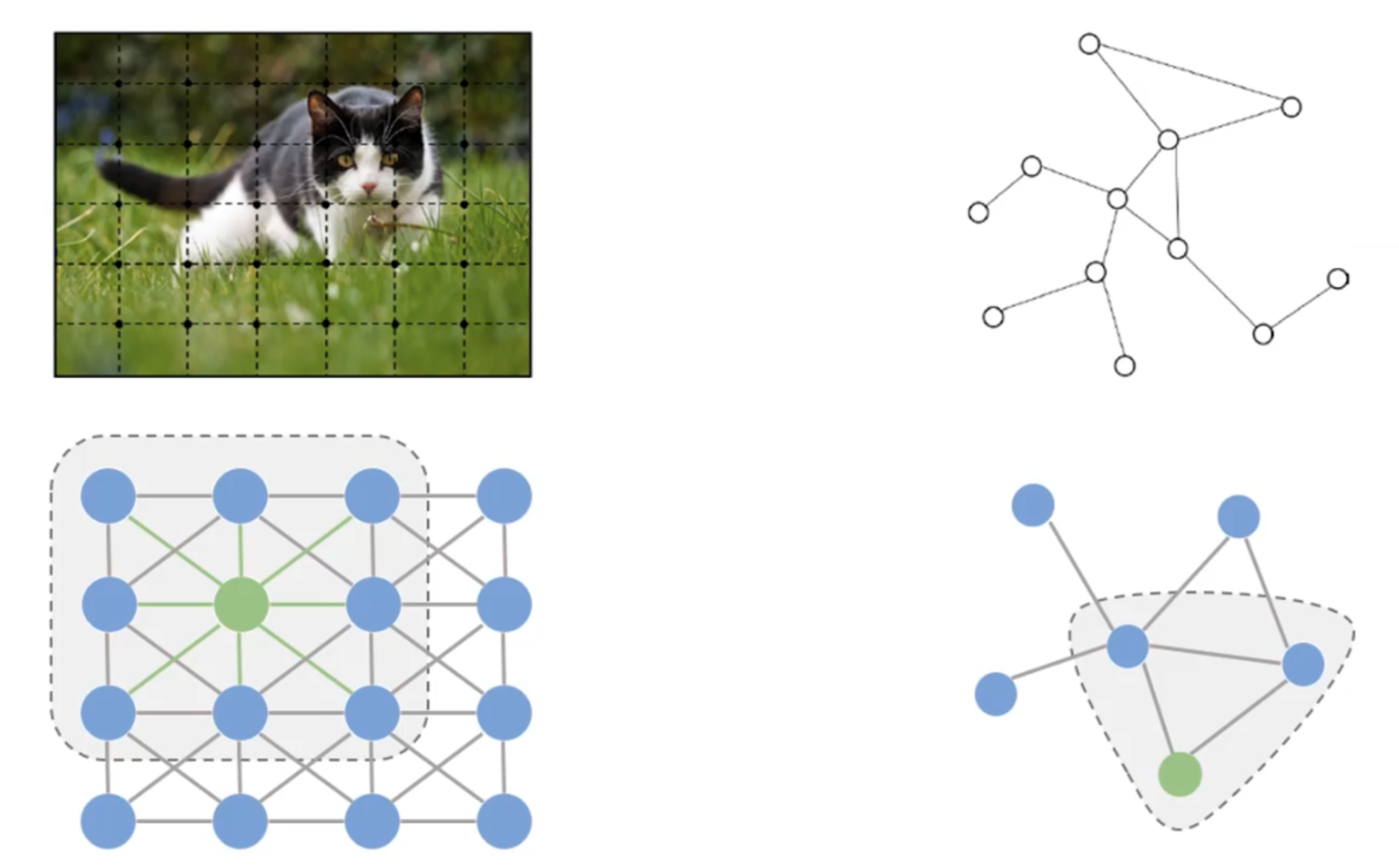
对于一张图来说我们可以把每一个像素点都看作是一个节点，然后我们把相邻的节点都连接起来会得到一个很规整的网络图。我们可以直接在它上面做卷积。相同的，如果不是一张图，而是任意的一个网络结构，我们也照猫画虎的可以选取一块区域做卷积。但是难点是我们选取的区域结构不同，卷积核如何确定？有两种方法，第一种是我们想一个办法来找一个可以随意变换的卷积核，第二种是我们把千奇百怪的网络结构序列化成一个统一的样式，这样就可以用一个common的卷积核来完成。

卷积有两种套路，一种套路叫空域卷积（spatial conv），另一种叫频域卷积。但是频域卷积的不足点很多，如今已经很少有人再去研究频域上的卷积了。所以我们只介绍一下在空域卷积中的实现方法。

第一种：设定可变长的卷积核

空域卷积是每次我们要求解的节点的参数都是通过空间上相邻的节点上的值得到的。那么空域卷积我们就要找到一个可变的卷积核。空域卷积有一个通用的框架，叫做message passing neural network(MPNN)， 它提出了一种更新参数的公式：

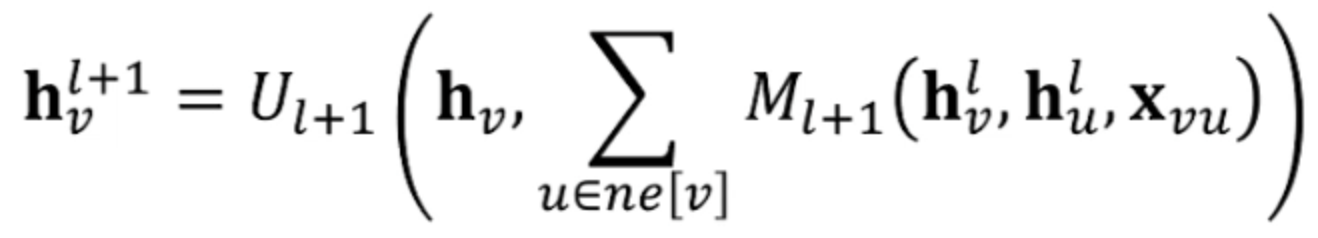
这个公式主要完成了两个步骤：1. 如何把邻居节点的信息传递给当前要更新的节点上；2. 如何通过邻居节点传递来的信息更新当前节点。其中M函数就代表了第一步的过程，我们可以认为是任意的一种操作（比如神经网络或者pooling甚至直接加权平均），通过加权来得到周围节点传递来的信息。U是第二步的函数，定义怎么去在下一时刻更新当前的节点v。

比如，GraphSage(graph sample and aggregate)就可以套用这个公式。在卷积的时候如果图很大，我们无法同时在整张图上进行卷积，所以GraphSage就提出我们可以先采样一些邻居，然后聚合这些邻居上的信息，最后就可以在节点上得到一个loss进行反向传播。

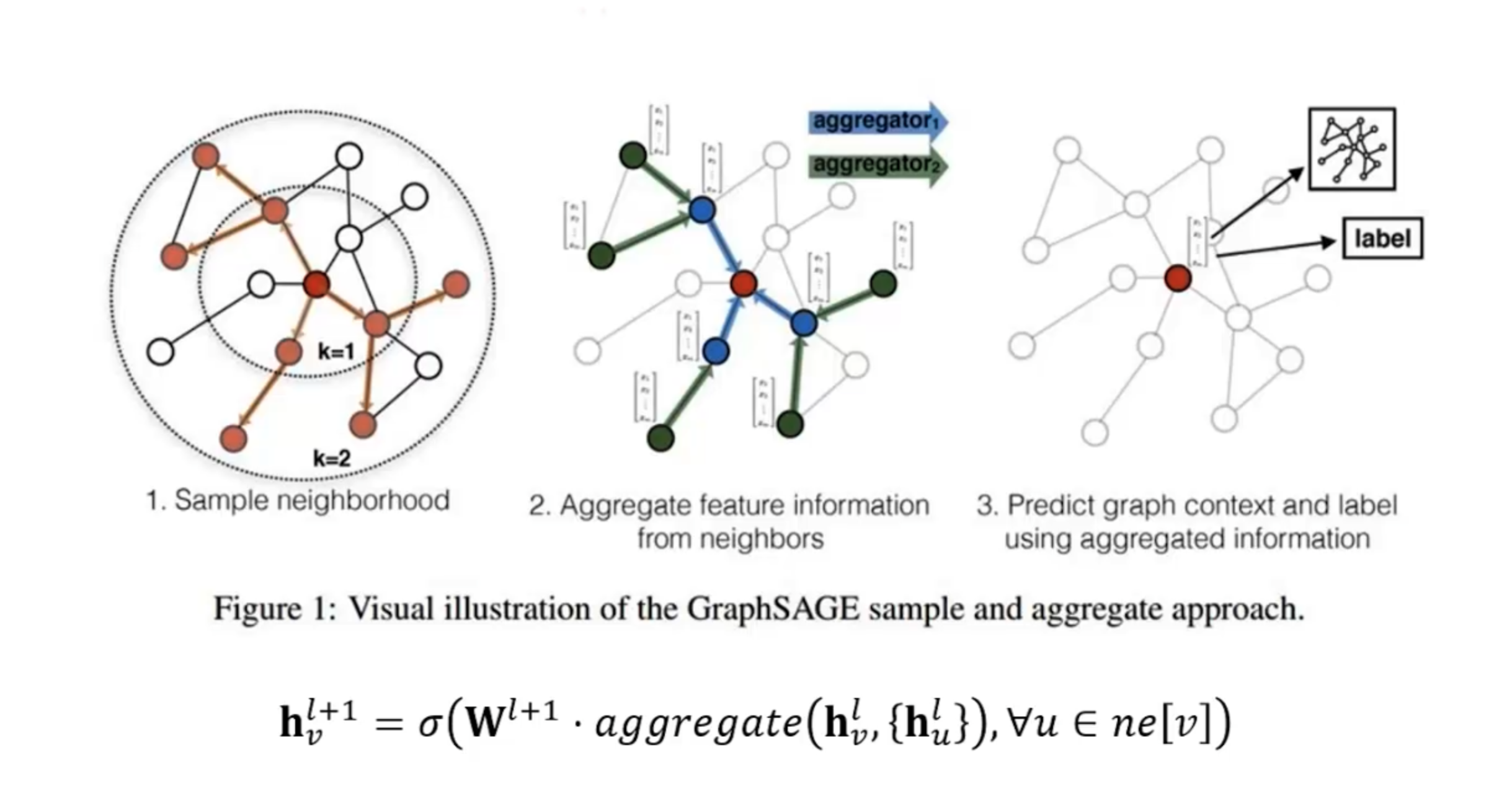
对于怎么设计这个聚合函数，可以自己定义，但是首先要考虑如何处理变长的信息。

第二种：序列化图结构

PATCHY-SAN是序列化一个图的方法。

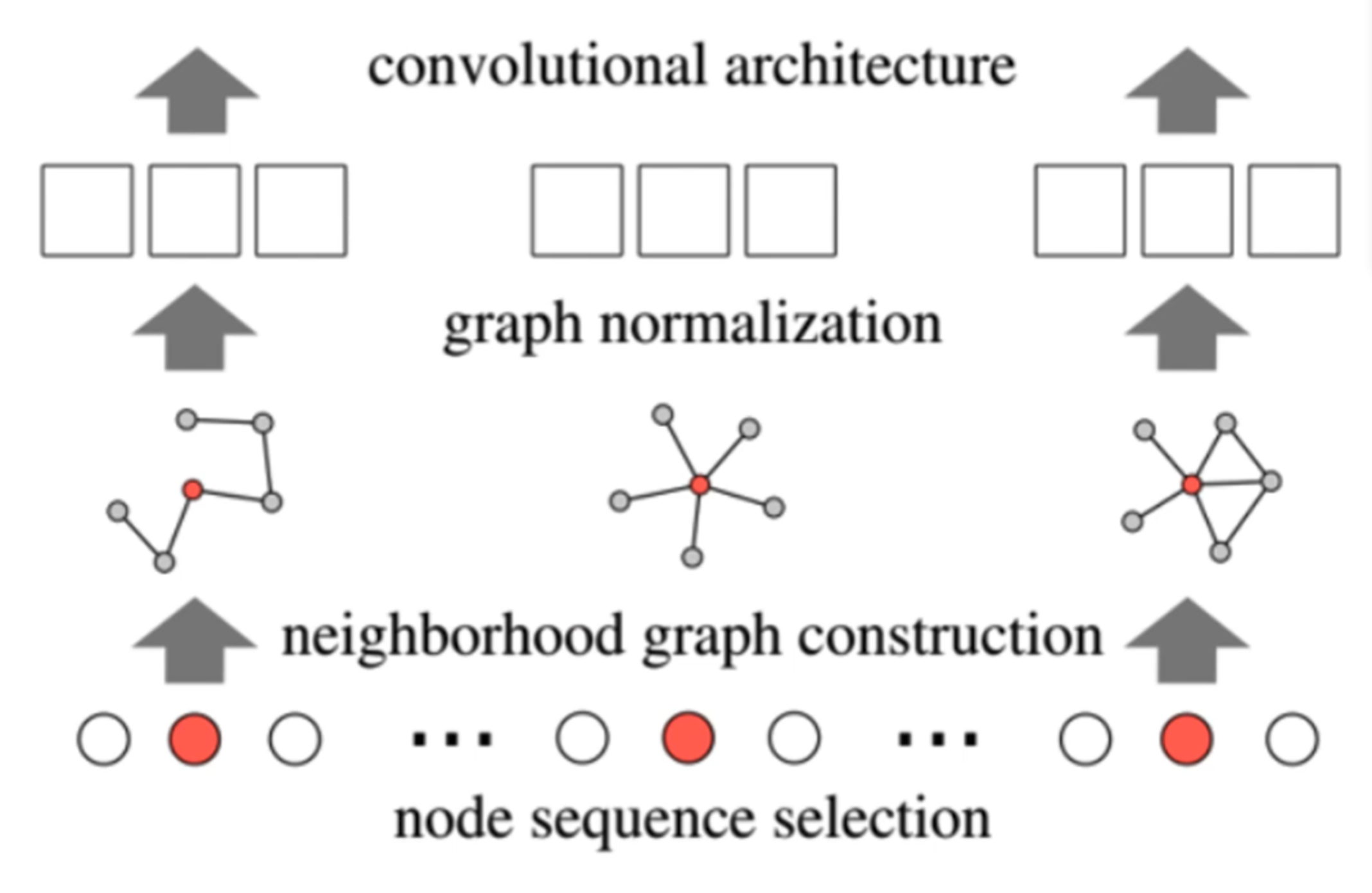
第一步我们要人为的定义一些规则来排序这些节点，越往前的越重要，也可以截取top k个节点，剩余的默认为对结果不造成影响。 第二步是我们从排好序的序列中的每个节点再选取top k个最重要的邻居，其余的扔掉。 第三步就是我们把每个k+1个一组的节点排排坐，这样就可以形成一个固定结构的图，然后再进行卷积操作。

Readout

那么最后我们无论用什么方法总之会得到每个节点的隐表示。那么得到之后如何计算出整个图的表示呢？

最简单的就是各种pooling的方式。例如avg pooling：假如有10个节点，每个节点我们学出了一个100维的向量，那么我们可以把每个节点的第i维向量求平均当作整个图的第i维的值。 还可以用学习的方法，在所有的node表示最后加一个全连接层，或者还可以添加一个全局节点最后用全局节点的表示当作图的表示。 当然还有其他各种更加炫酷的方式，例如可微池化differetiable pooling等。