宏观理解
Conditional random field (条件随机场)和HMM很像,比如都可以用维特比算法求解。下图更好的展示了几种模型之间的关系。
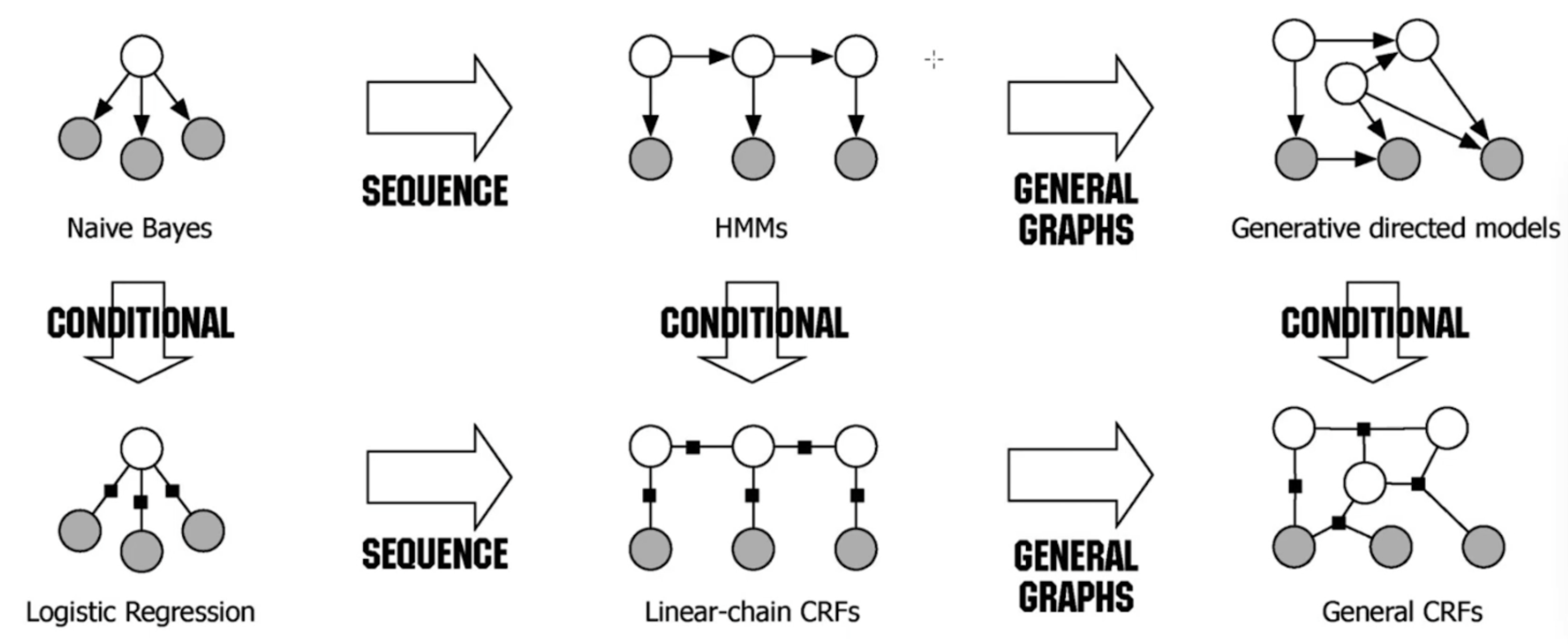
上层模型都属于生成模型,求解通过最大化联合概率。下层模型都属于判别模型,求解通过最大化条件概率。不代表所有判别模型都必须是无向图!!
从朴素贝叶斯开始往右看,它是没有时间维度的,但是如果我们在它的后面再加几个朴素贝叶斯,延展开来就是HMM。但是HMM是有马尔可夫假设的,也就是当前点只依赖于前一个节点,那么如果我们抛弃这条假设的话,就变成了贝叶斯网络.
从朴素贝叶斯往下看,把朴素贝叶斯转换成判别模型,就变成了逻辑回归。我们把多个逻辑回归合并在一起,就变成了线性链条件随机场。如果我们再把限定条件去掉,那就是General CRF。
有向图vs无向图
顾名思义,有方向的叫有向图,无所谓方向的叫无向图。所以在选择图模型的时候就要知道他们之间的区别:
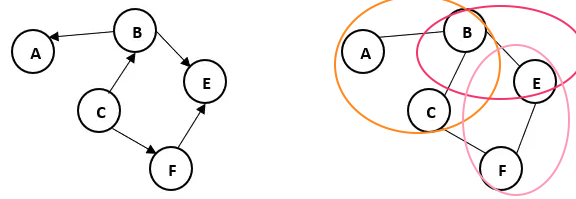
- 变量之间是不是有关系,比如人际关系网就要用有向图来表示,a的父亲是b,b的父亲不能是a。
- 在优化上,像MEMM这种有向图会有label bias problem。我们就需要把它转化成无向图来解决。
- 在计算上,我们在求联合概率P(A,B,C,E,F)的时候,有向图就很好表示P(A,B,C,E,F) = P(C) P(B|C) P(F|C) P(E|B,F)…连乘的方式。 在无向图中,我们要首先把图根据最大团的方式分成几个模块,然后再把这些模块的分数相乘
。每一个ϕ表示的是这几个节点捆绑在一起的分数(scoring function/compatibility),每一个的分数越高越好。其中的Z其实就是一个归一化的作用,为了把分数映射到概率上。当然我们也可以假设其中每两个(pair-wise)固定在一起。
微观分析
在HMM中,我们知道每个观测都是依赖于对应的隐变量的。那么假如我们在做的是词性分析中,我们不能只依靠一个单词就给判定词性,更好的是依据上下文。
所以我们把一般的HMM改写成下图,对于每一个观测变量,都可能由所有的隐变量给出。此时的目标函数就写成。但是此时仍然有一个问题,就是公式后半部分的发射概率计算量太大了。
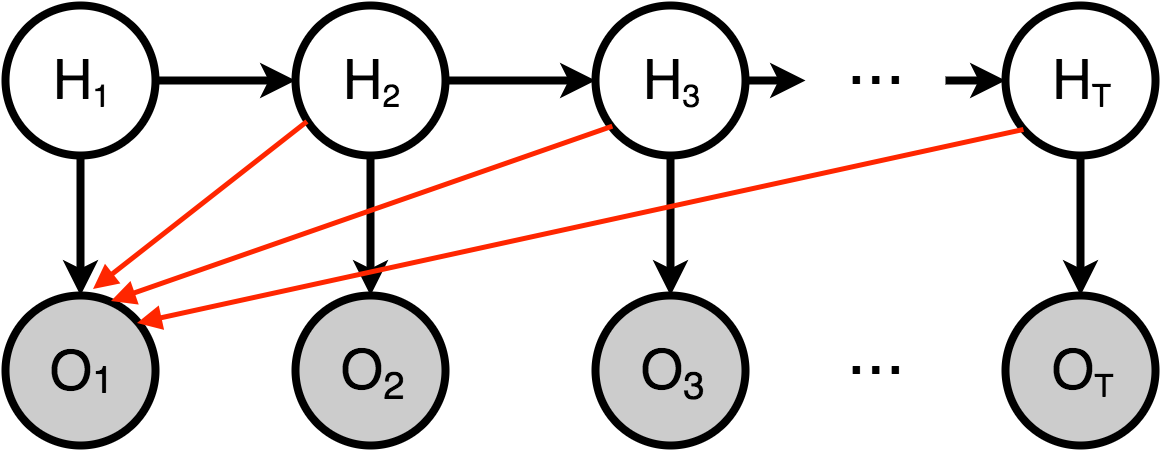
那么我们就想,可不可以把它从生成模型改造成一个判别模型,也就是要求P(z|x)。从而我们就有了MEMM模型:

此时我们的目标函数写作。那么我们要找到的最佳的z就是在给定x和前一个z的时候,下一个z的argmax。但是此刻我们卡住了,因为我们会遇到一个bug叫做Label Bias Problem。
Label Bias Problem
在下面的图中,我们一眼就可以看出来路径最好的是state1–>state1–>state1–>state1。因为他们路径的概率乘积最大。 但是不公平啊,从state1出来的路径才有2条,那么因为他们的sum必须是1所以每条路径的概率都会比从state2出来的5条路径大啊。所以这样的话岂不是永远最佳的路径都是出度小的state吗?
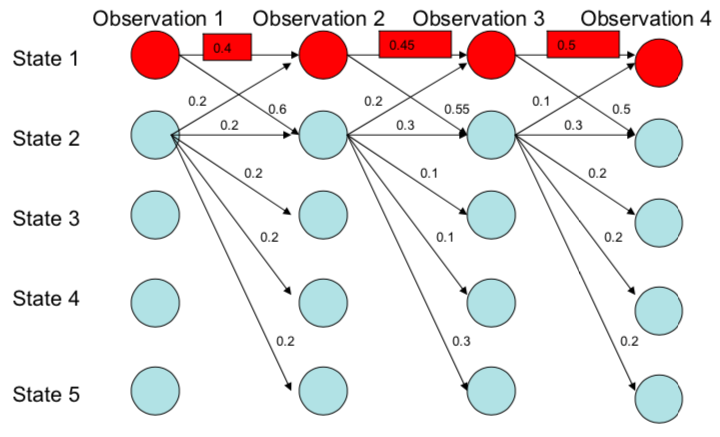
这个问题的核心就是出现了local normalization。那么我们怎么去改变它呢?我们可以把他们的每条边的转移概率改成分数的形式:
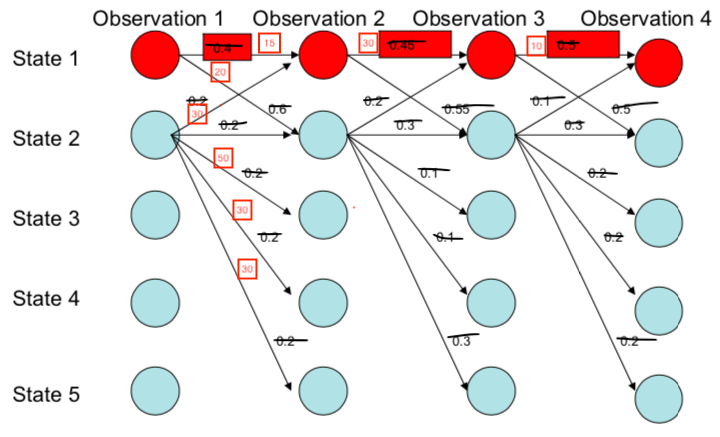
怎么改造呢?那就是把有向图改造成了无向图。此时我们的模型变成了CRF。那么怎么计算这些分数呢?也就是我们之前所说的scoring function。
Log-linear Model
我们知道ϕ代表的是变量之间的compatibility,所以变量之间关系越紧密,ϕ的值会越大。那如何求得这个scoring function呢?
既然关系越紧密值越大,那就是说我们需要设定一些特征,然后看这些特征应用到这些变量之间谁和谁组合之后会更大。我们先不管如何去做这些特征工程。假定我们已经有了f1,f2,f3等等的features,那么我们可以让ϕ(a,b,c) = w1f1 + w2f2 + w3f3 +…+ wnfn + b。w就是我们的参数,也可能会有一个偏置b。至于我们的特征工程该如何做,一般分两种,一种是自己手工做,也就是传统的CRF;另一种是用模型学出来,比如LSTM/Bert这种深度学习模型,那就是LSTM/Bert-CRF了。所以说我们的scoring function怎么定义,得出来的模型的种类也是不一样的。
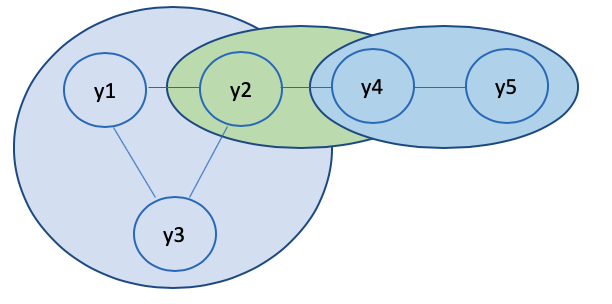
假设我们现在有这样一个log-linear model。并且我们根据最大团把它分成了3个部分。它的联合概率则是
其中c是循环每一个团,所以ϕc和yc也就是相应属于该团的y和ϕ值。因为我们要保证每个score必须是正数,所以我们可以继续把每个团的ϕ定义为:
其中J是总共的特征个数,F是具体的特征,这个特征是公用的,所有的团使用相同的特征。我们在现在的基础上加上一个log,即:
前面是log,后面是linear,所以我们管它叫做log-linear model。
从Log-linear Model到CRF
我们知道了log linear model的形式为
其中归一化项Z我们可以写成也就是所有y的形式的总和。
Fj(x,y)代表从(x, y)里提取第j个特征。
我们有一个CRF模型如下:
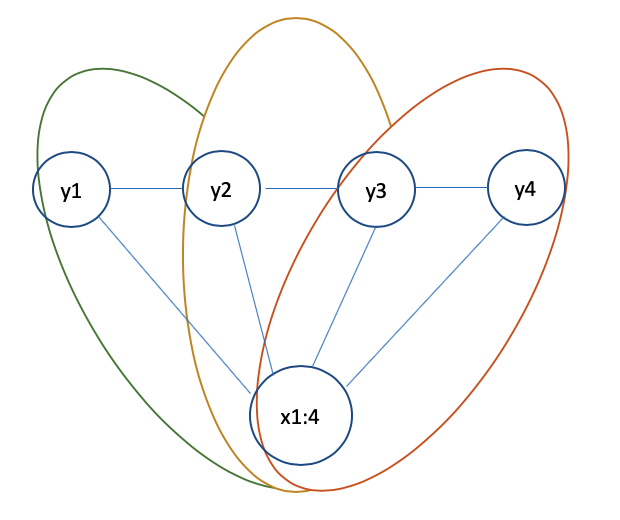
一共有3个不同的最大团,所以我们让T代表时刻的话,i一共有T-1个,所以从2开始循环每个团。所以我们有了以下这个linear CRF的条件概率。
我们在这个公式里面唯一未知的变量就是w,因为f是我们自己定义的特征,所以我们是知道的。所以在给定数据集D的情况下我们可以使用最大似然 + 随机梯度下降来求得参数w。
在求得了参数之后,就可以用参数和x来判别y了。
我们用来代替后面的项。但是问题是yi只是一个占位符,它实际可以被很多种y1,y2,y3,… yn的组合被替代,那么如果找出全部的组合方式计算时间复杂度太高了,所以我们就得用维特比算法来解决这个问题。
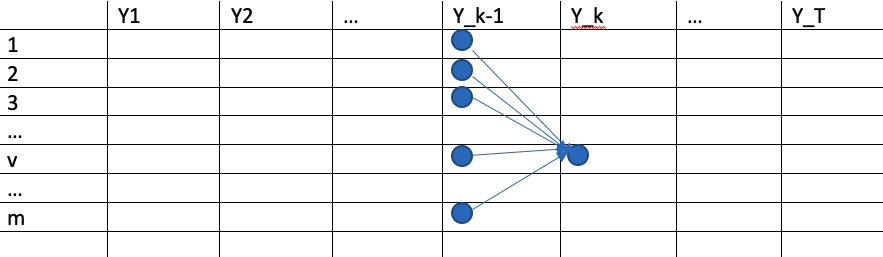
比如我们要求的是在k时刻的v节点的值,我们写作U(k,v)。根据维特比/动态规划算法的定义,我们确保了之前的路径从时刻y1到y_k-1都是最优的,那么我们只需要找到从y_k-1到yk最优的m条路径中的一条即可。所以我们可以写成
其中s是上一步y_k-1时刻最优的节点,然后通过一个函数g来选择最大值。
