宏观理解
Hidden Markov Model是一个在自然语言处理应用很广泛的时序概率模型。它的所有隐变量都由一条马尔可夫链生成,并且每一个隐变量的状态只依赖于相邻的隐变量,形成一个链状的依赖关系。
说的这里就要扯一下著名的马尔可夫假设了:
- 每个隐变量只依赖于前一个隐变量
- 每个观测变量都是相互独立的,只和当前隐变量有关。
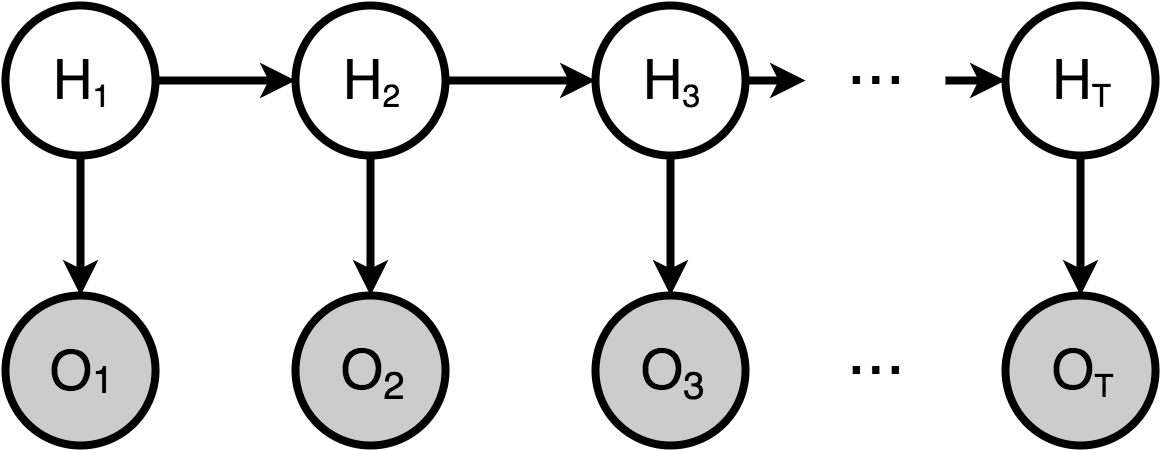
其中我们把上层马尔可夫链随机生成的状态序列叫做状态序列(state sequence),每个状态生成一个观测,而由此产生的观测的随机序列称为观测序列(observation sequence)。 例如下层中的每个圆圈。序列的每一个位置也可以看作是某一个时刻。
微观分析
在深入之前,我们先定义几个符号,我们用
- Q来表示所有的状态集合,也就是上层序列:Q = {q1,q2,q3,…,qn}
- V来表示所有可能的观测集合,也就是下层序列:V = {v1,v2,v3,…,vm}
- N来表示可能的状态数量
- M来表示可能的观测数量
- I来表示长度为T的状态序列
- O来表示与I对应的观测序列
- π来表示初始状态概率向量(1*N):时刻t=1处于状态qi的概率
- A来表示状态转移概率矩阵(N*N):时刻t处于状态qi的条件下时刻t+1转移到状态qj的概率
- B来表示观测概率矩阵(N*M):时刻t处于状态qj的条件下生成观测vk的概率
HMM可以解决三种问题:
- 概率计算问题:给定模型λ = (A,B,π)和观测序列O = (o1,o2,...,oT),计算该观测序列出现的概率P(O|λ)。例如语言模型。
- 学习问题:已知观测序列O = (o1,o2,...,oT),估计模型λ = (A,B,π)的参数,使得在该模型下观测序列概率P(O|λ)最大。
- 预测问题:已知模型和观测序列O = (o1,o2,...,oT),求对给定观测序列条件概率P(I|O)最大的状态序列I = (i1,i2,...,iT)。例如词性标注。
概率计算问题
我们已知的是模型的三个参数矩阵,也知道来观测序列,需要计算的是观测序列出现的概率。
如果我们直接去愣算的话思路很清晰。那么想知道观测序列,我们就得先知道状态序列。因为观测变量是由隐变量生成的。 所以我们可以遍历所有可能的隐状态序列I,使用π和A矩阵求对固定的状态序列I,观测序列O的概率是:
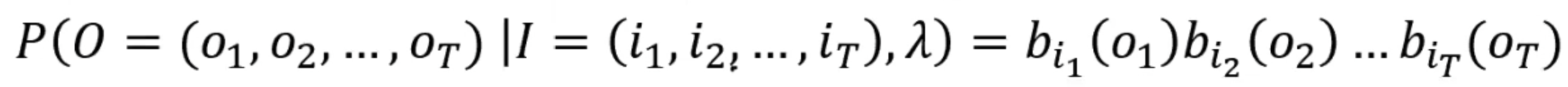
好,那么我们现在需要的是求他们的联合概率P(O,I|λ) = P(O|I,λ)P(I|λ)。已经求出来P(O|I,λ)了,那么P(I|λ)就是状态序列I = {i1,i2, ..., iT} 的概率:
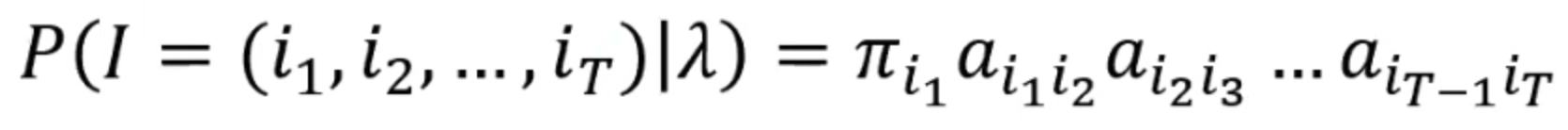
好,然后我们就知道了P(O,I|λ)的值:
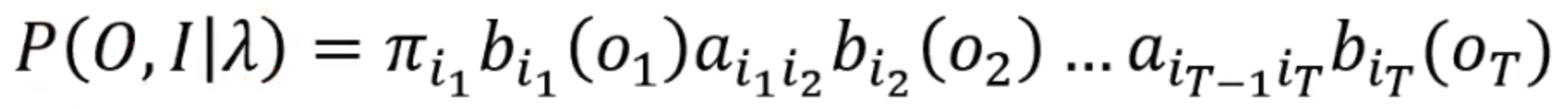
最后就是对所有可能的状态序列求和,得到P(O|λ):
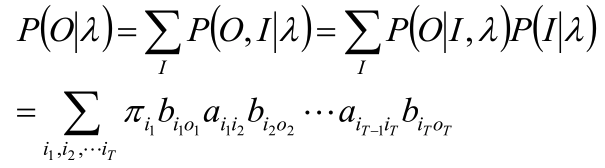
但是计算量是指数级的。随后有人就提出来一个基于动态规划的改进算法:前向算法。
我们首先定义一个概念什么是前向概率:在给定模型λ = (A,B,π),时刻t的部分观测序列为o1,o2,…,oT,且状态为qi的概率为前向概率。
好,定义往往都不是人话,我来翻译一下:现在我们已经有了一个模型包括三个参数矩阵,因为HMM是一个时序模型,所以存在很多个时刻,我们随机一个时刻t,那在这个时刻t 之前的观测序列就是o1,o2,…,ot,既然有观测序列那肯定也有隐状态序列,但是定义只规定了在观测变量为ot的时候的隐变量为qi,至于前面的o1,o2,…,ot-1的隐变量是什么 我们不管。所以在这种情况下的概率,我们叫做前向概率。
那我们就想,既然有qi的前向概率,那它的前面就会有q1,q2,q3等等的前向概率。那么我们把他们加起来,一直加到qi-1是不是就是qi的前向概率了?那qi的前向概率不就是 观测序列从o1,o2,…,ot的生成概率嘛!
好,那我们如果知道前向概率的递推公式了,是不是就可以从任意时刻点开始想推到哪就推到哪了。
好,那么在递推之前,我们要有一个初始点,也就是t = 1的时刻,我们可以计算出它的前向概率就是时刻1的隐状态并且产生观测状态o1的概率:
然后我们递推到下一个2时刻的前向概率时,它有2时刻对应的隐状态qi,我们在上一步初始化了隐状态的概率,现在要移动到下一个时刻,我们就用转移矩阵计算从时刻1的隐状态转移到时刻2的隐状态的概率,
之后又到了时刻3,也有对应的隐状态,但是此时时刻1和时刻2的隐状态都有可能直接转移到时刻3的隐状态,所以我们就需要sum他们每一个的转移概率:
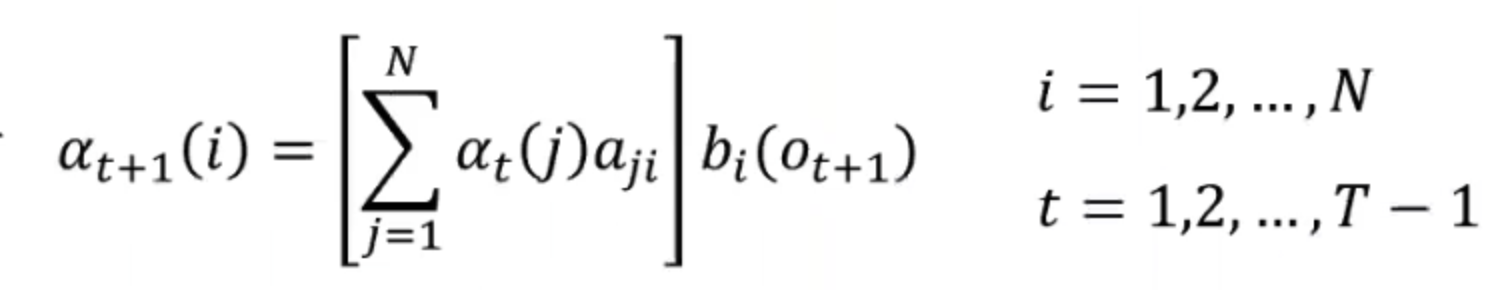
j就是每一个之前可能转移到当前隐状态的隐状态。
那么后向算法的后向概率就是前向概率反过来,所以在求第t时刻有第i个状态的概率 = t时刻的前向概率 * t时刻的后向概率,即: P(it = qi,Y|λ) = αi(t) * βi(t)
学习问题
既然是学习问题,就分有监督和无监督两种学习问题,对于有监督来说已知训练数据包含S个长度相同的观测序列和对应的状态序列,估计模型λ = (A,B,π)的参数。那么 对于参数矩阵A,B我们只需要数一下即可。
那么对于非监督学习问题,就是已知观测序列O = (o1,o2,…,oT),而没有对应的状态序列,估计模型λ = (A,B,π)的参数。 那么这个问题就变成了EM算法对于模型参数的估计问题。
Baum–Welch算法
Baum–Welch是EM算法在隐马尔可夫模型中的一个具体的实现。 那么EM算法中我们分为4步进行计算:
- 1. 初始化状态序列
- 2. 对数似然函数,在HMM中我们可以写成logP(O,I|λ)
- 3. 计算Q函数并分别更新三个参数矩阵,引入拉格朗日乘子法辅助求得:
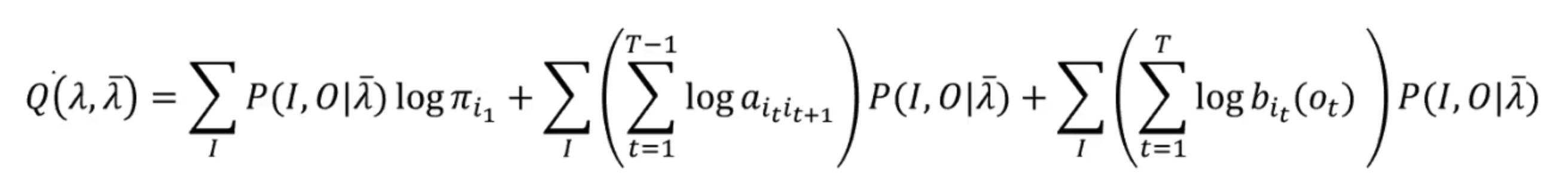
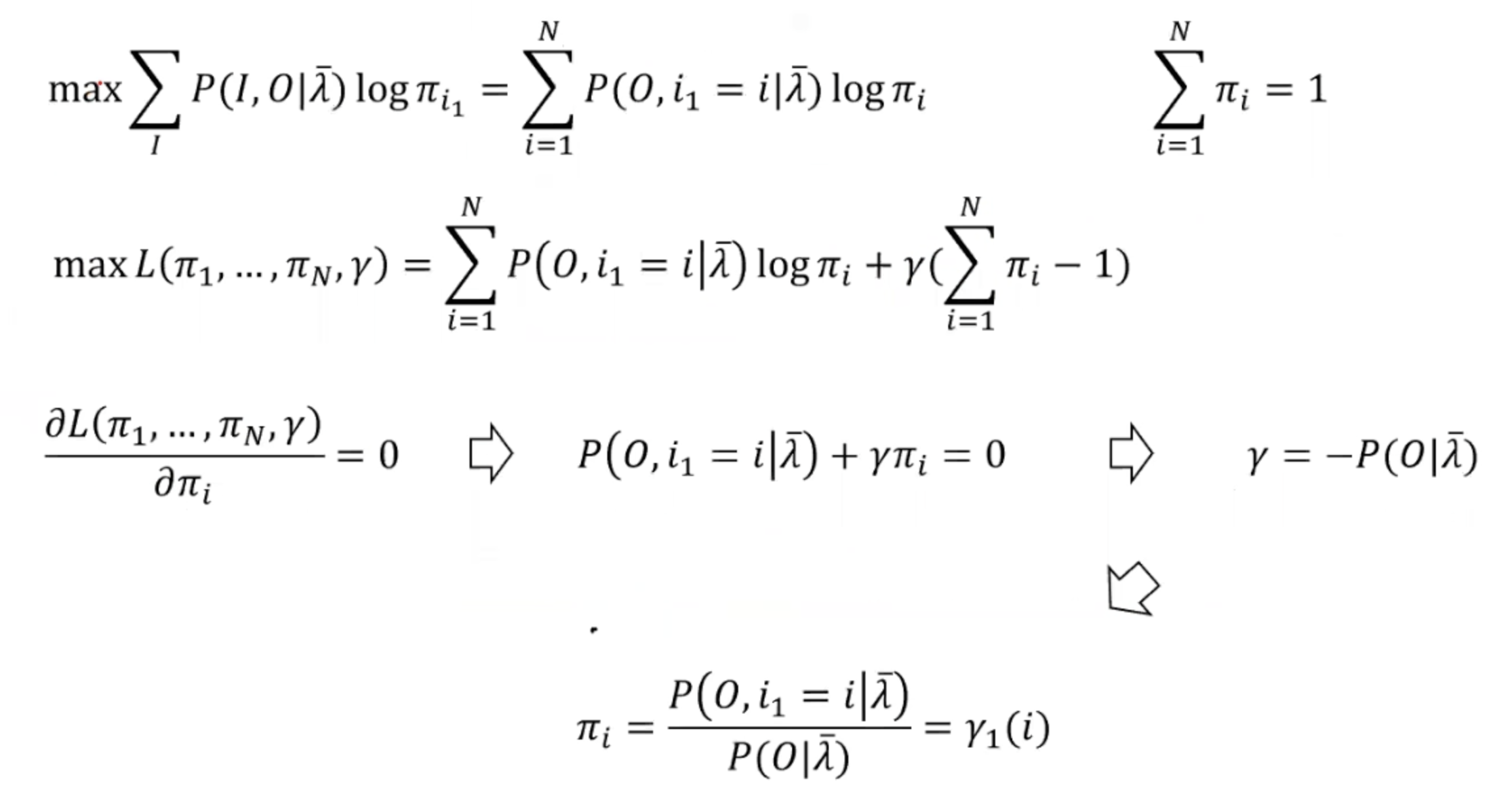
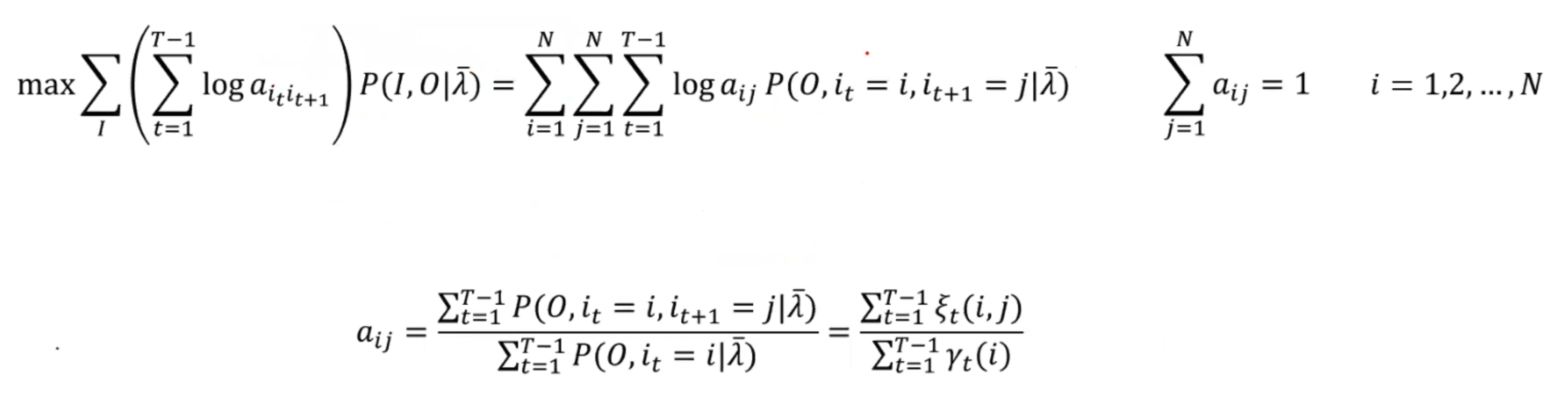
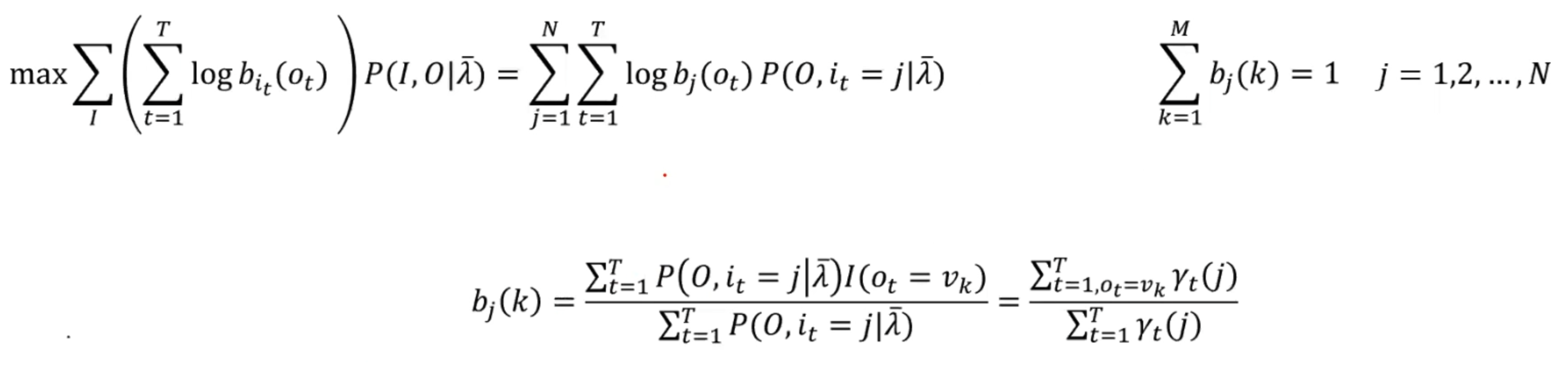
- 回到第二步,直至收敛。
预测问题
即已知模型和观测序列O = (o1,o2,...,oT),求对给定观测序列条件概率P(I|O)最大的状态序列I = (i1,i2,...,iT)。
我们可以用一个近似算法:在每个时刻t选择在该时刻最有可能出现的状态,从而得到状态序列
:
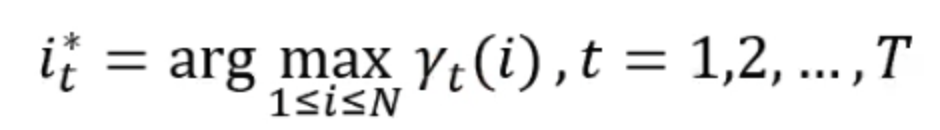
所有优点就是计算很简便,但是我们无法保证每个是非0的,所以通常来讲我们用的是维特比算法。
Viterbi算法
维特比算法是一种动态规划算法。它用于寻找最有可能产生观测事件序列的维特比路径——隐含状态序列,特别是在马尔可夫信息源上下文和隐马尔可夫模型中
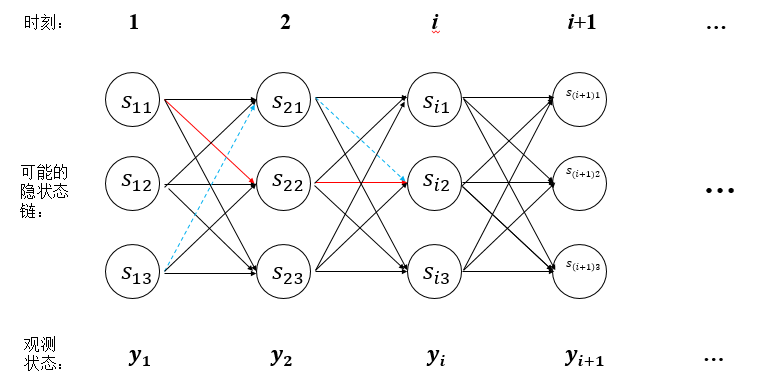
例如在上图中,我们要求从时刻0开始,每往前走一个时刻,都要保证是目前为止最优的。但是因为我们要找的是路径,所以还要保存好每次的上一个节点。

所以我们整体的算法为:

