宏观理解

EM算法（Expectation-maximization algorithm）是用来在概率模型中寻找参数最大似然估计的算法，其中概率模型依赖于无法观测的隐变量，比如说HMM隐马尔科夫模型。看不懂这句话什么意思没关系，看完下面两个案例相信你就明白了。 EM算法是一种迭代优化策略，由于它的计算方法中每一次迭代都分两步，其中一个为期望步（E步），另一个为极大步（M步），所以被称为EM算法。 基本思想：

1. 根据己经给出的观测数据估计出模型参数的值
2. 根据上一步估计出的参数值估计缺失数据的值
3. 根据估计出的缺失数据加上之前己经观测到的数据重新再对参数值进行估计
4. 返回到步骤1，直至最后收敛，迭代结束。

微观分析

背景：你跟一个导师在做一个社会调研，课题是研究不同城市的男女身高分布。你手上现在有其中某一个城市收集出来的数据，一共有1000条，500条男性身高数据，500条女性身高数据。

最大似然估计

导师突然走进来说：“你把这些数据统计一下吧，然后发布一个正态分布的模型。”
你说：“好，那这个模型的参数是什么？”
导师说：“算算咯，你可以用一下最大似然估计。”


当我们有了两个已知条件（1）样本的概率分布（2）样本，就可以求出来分布模型的参数。
在导师给你的资料中，我们首先确定了它是服从正态分布的，我们又知道样本，那么此时我们缺的就是正态分布的参数也就是均值和方差。
在导师给你的问题中，每条男女生的身高数据是独立的，也就是说数据间互不影响，一个自然的想法是从这个分布中抽出一个具有n个值的采样X1,X2,…,Xn， 然后用这些采样数据来估计θ。

那么按照最大似然估计求解参数的步骤

1. 我们需要写出一个最大似然函数

   

2. 对上面的似然函数求对数

   

3. 对上式求导，设导数为0，解出参数值即可

所以总结来讲，我们多数情况下是根据已知条件来推算结果，而极大似然估计是已知结果，寻求使该结果出现的可能性最大的参数值。

EM算法

第二天导师又慌慌张张突然跑进来说：“哎呀我昨天喝茶不小心把这1000条数据的男女标签给泡了，已经看不出来了怎么办啊？”
你沉思了一下说：“教授莫慌，我觉得还可以补救一下！”
导师满含泪光地望着你：“真的吗？可是哪条数据属于男还是女都不知道了，这些数据还怎么用啊？”
你说：“不急，让我来用EM算法试一波。”

首先明确一下两个符号，通常我们把隐变量用z来表示，隐变量就是不能观测到的数据；把观测变量用y表示，观测变量就是已知的可以观测到的数据。 所以在你的手上，被导师泡了的标签我们可以认为是隐变量，没有被泡到的所有身高数据我们可以认为是观测变量。

1. 你随便给两个参数均值和方差瞎蒙了一个初始值，男女生各一套参数，各一套分布
2. （E步）根据你蒙的（或从3更新后的）参数值建模，循环1000条数据，看每一条数据大概率可能属于男生分布还是女生分布
3. （M步）通过你在第二轮选出来的男生分布中的数据重新更新两个参数均值和方差（依靠最大似然估计），女生也一样
4. 返回第2步，直到参数不再发生变化

完美！ 此时你既有了隐变量的男女生标签，又通过最大似然估计求得出了分布参数。

EM算法数学推导

complete case：(z,y)两个变量都可以被观测到，他的对数似然函数写作

incomplete case：(z)不可以被观测到但是(y)可以，他的对数似然函数写作

所以在incomplete case中我们的目的就是寻找一个θ和z可以让l(θ)最大化。

那么整个EM算法可以迭代如下：

1. 选择模型参数的初始值
2. E步：记为第i次迭代后模型参数的值，在第i+1次迭代的E步，计算期望：

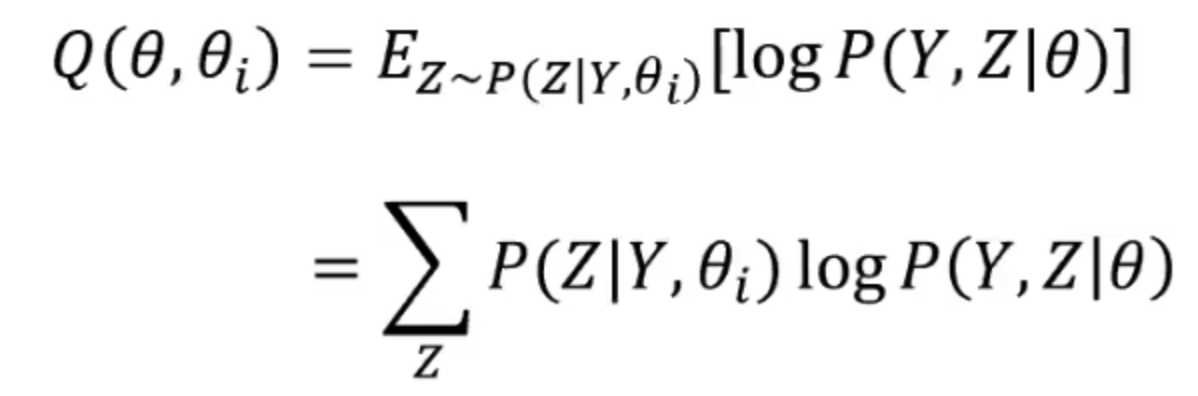
1. M步：求使得极大化的θ，确定第i+1次迭代的参数的估计值
2. 重复2-3步，直到收敛

所以到目前我们懵逼的地方就是那个Q函数，那是什么玩意？

我们已经知道我们要求解的对数似然函数l(θ)，我们的目的就是让l(θ)越大越好。所以我们期望在每次参数更新后的l(θ)都要比上一轮更新后的要大一点点。故我们希望的是:

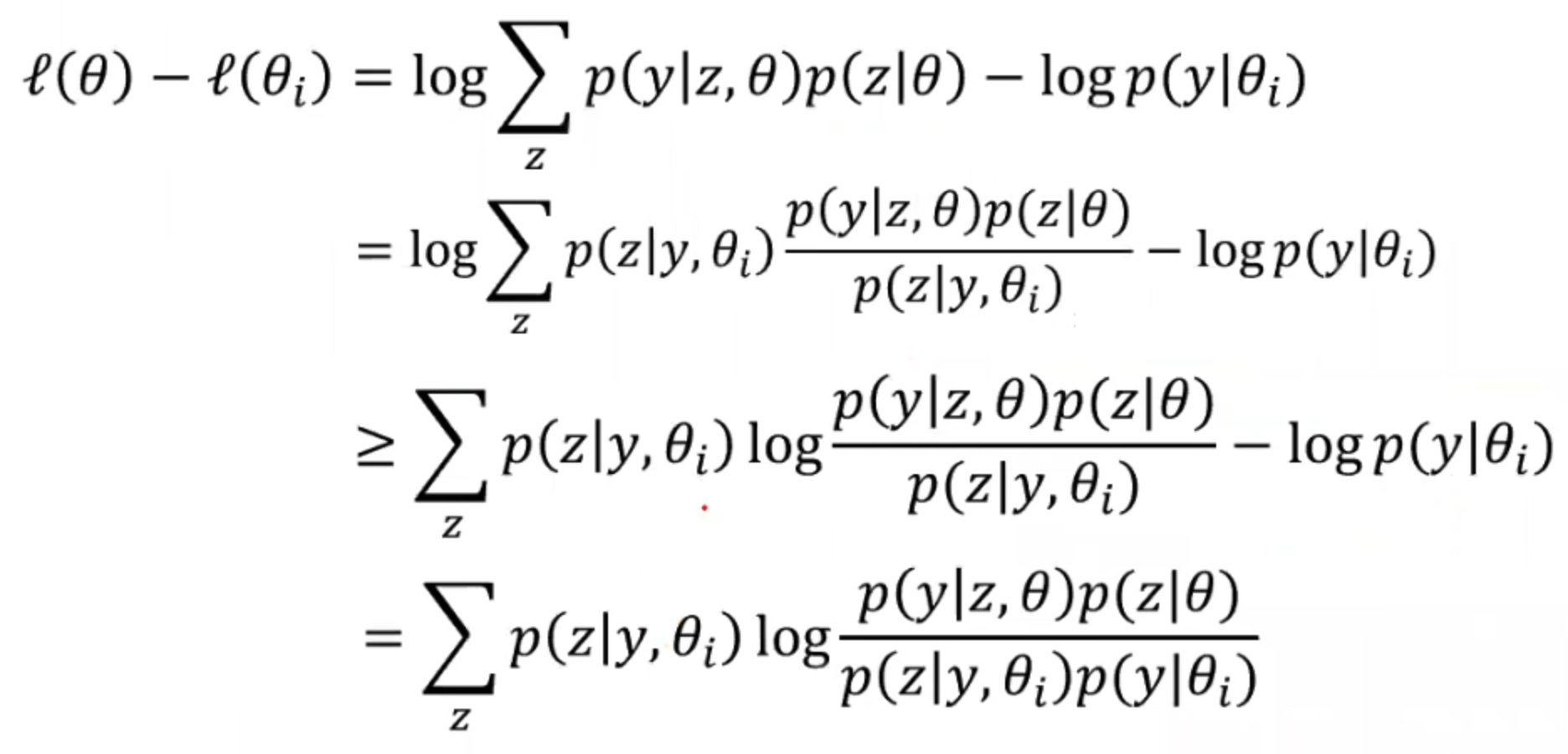
在第二步中我们用一个trick，就是左半部分我们先乘再除一个。 然后因为在第三步中变成的log sum是很难求的，所以我们引入另一个辅助叫Jensen不等式：

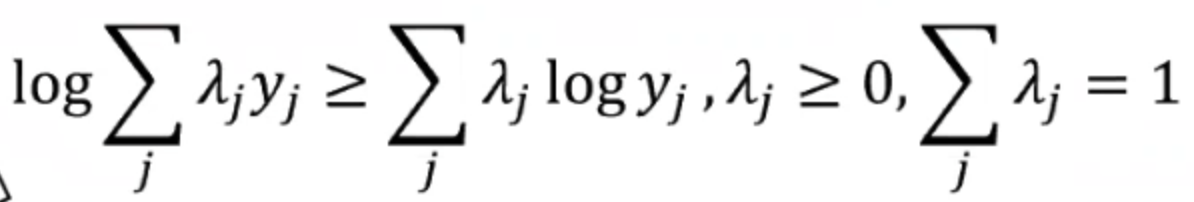
所以我们把不等式代入到第三步的左半部分，用来代替

所以通过上面的推导，我们可以得出一个结论，就是

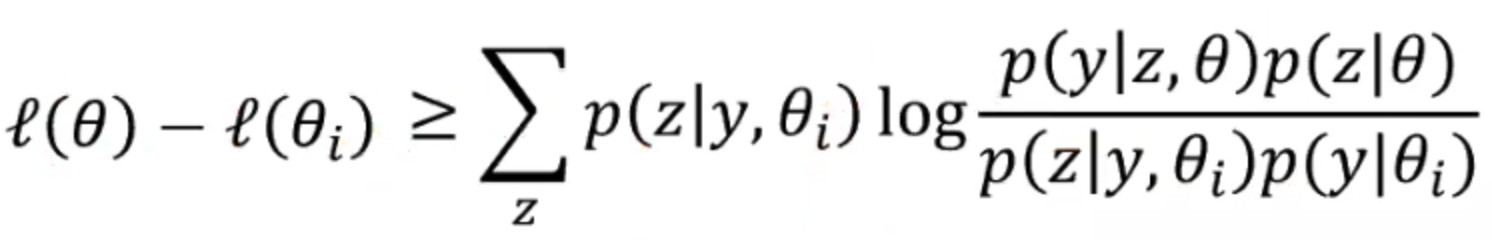
为了书写简便，我们用B来代替，所以上式就变成了下面的公式(1)；我们也就能得出公式(2)。

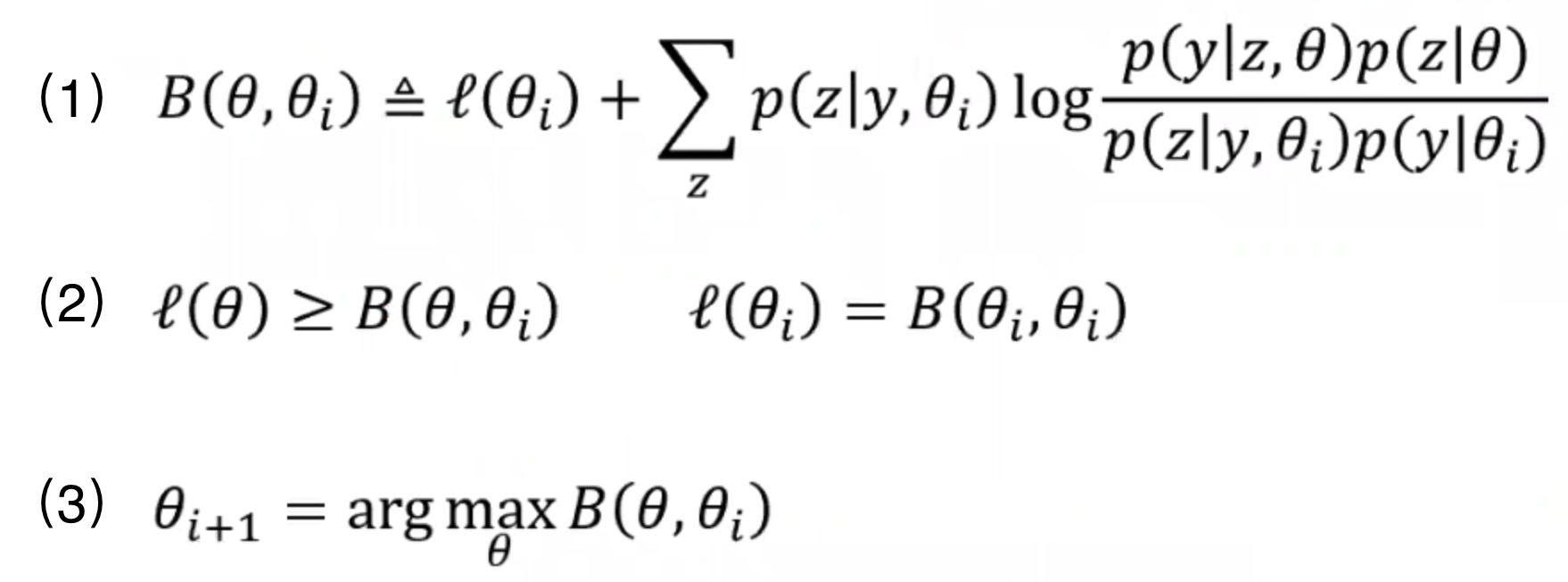
在每次迭代的时候我们都想让下一次比上一次大，所以可以得出公式(3)。故而我们可以展开argmax来看看如果最大化这个上一轮的θ。

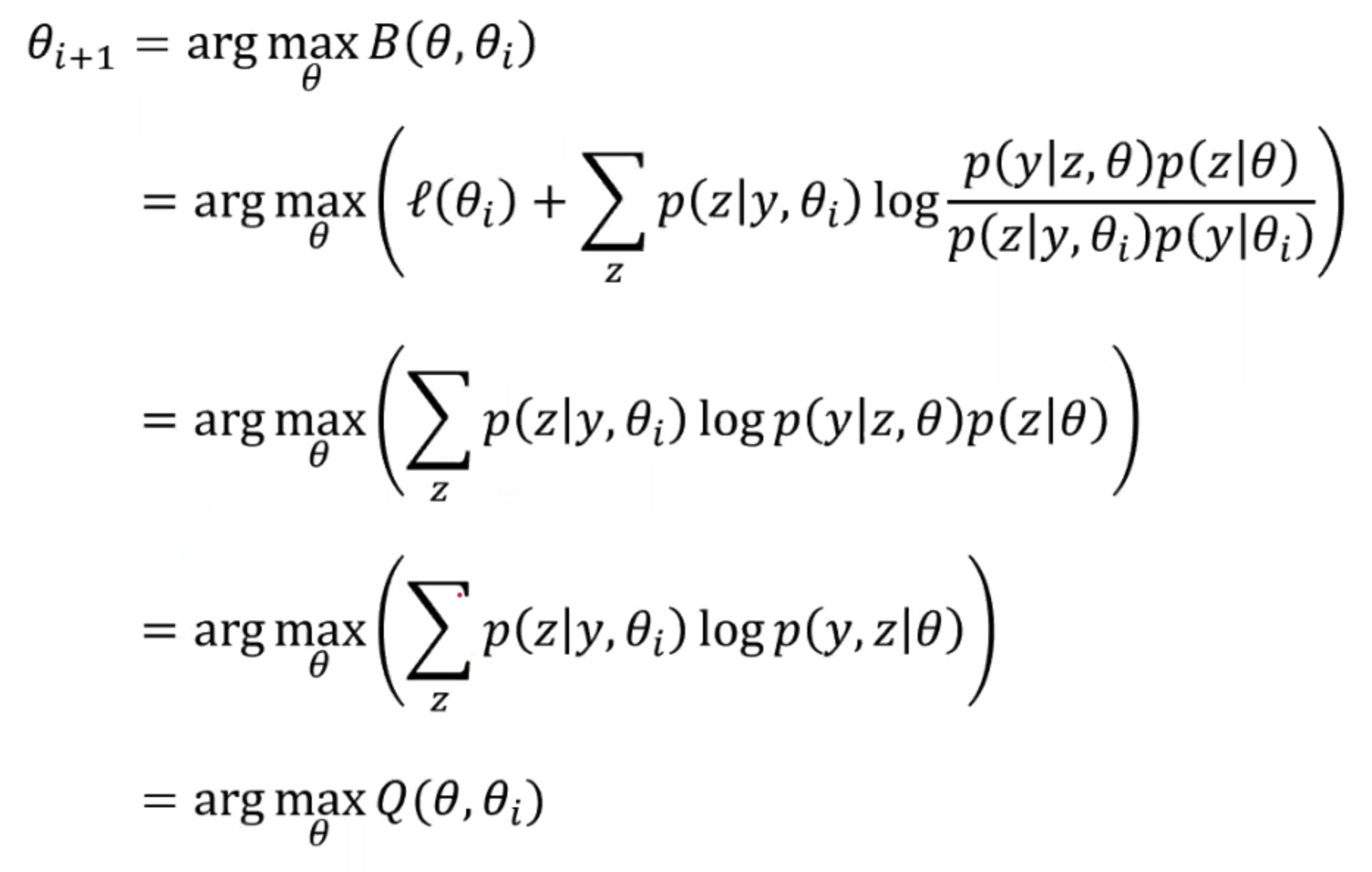
所以我们发现最后我们要极大的函数就是之前的Q函数。所以在迭代的时候，只要我们可以最大化Q函数，也就能得到一个更好的参数。