宏观理解

Optimization is the core of Machine Learning！
对于每个人工智能问题，都是在解决模型和优化这两个难点。所以对于训练模型来说，在做的就是找到模型参数，这个过程就是通过优化算法。比如说SVM就是一个凸优化问题。 对于所有的优化问题，我们都可以写成要Minimize f(x)的形式，f就是目标函数。他也可能会有一些限制条件，比如目标函数中的某些算式是小于等于0的，或等于0的。也就是一个是不等式约束，一个是等式约束。 对于任何其他种类的目标函数，也都是可以改造成这个形式。
对于优化问题我们可以分为4个种类：

• 凸函数convex vs 非凸函数non-convex
• 连续的continues vs 离散的discrete
• 有约束constrained vs 无约束的non-constrained
• 平滑的smooth vs 不平滑的non-smooth
  其中最简单的优化问题就是凸函数、连续的、没有约束并且是平滑的。
  我们本次只讨论凸函数的优化。

微观分析

我们想把一个复杂的问题变成可以进行凸优化的问题是因为凸函数只有一个local optimal，也就是global optimal。 对于非凸函数的优化，就会有很多个局部最优解，不一定可以找到全局最优解。所以如果碰到了非凸函数的优化问题，比如说深度学习， 我们往往会追求一个更好的局部最优解。所以对于深度学习来说，模型的预训练变得非常重要，因为一个好的预训练可以帮助你找到更好的local optimal。 或者我们可以尝试把一个非凸函数松弛(relax)成一个凸函数。甚至如果数据很小，也可以去尝试暴力解决。

什么是凸集？

对于一个优化问题，我们都可以写成如下形式：

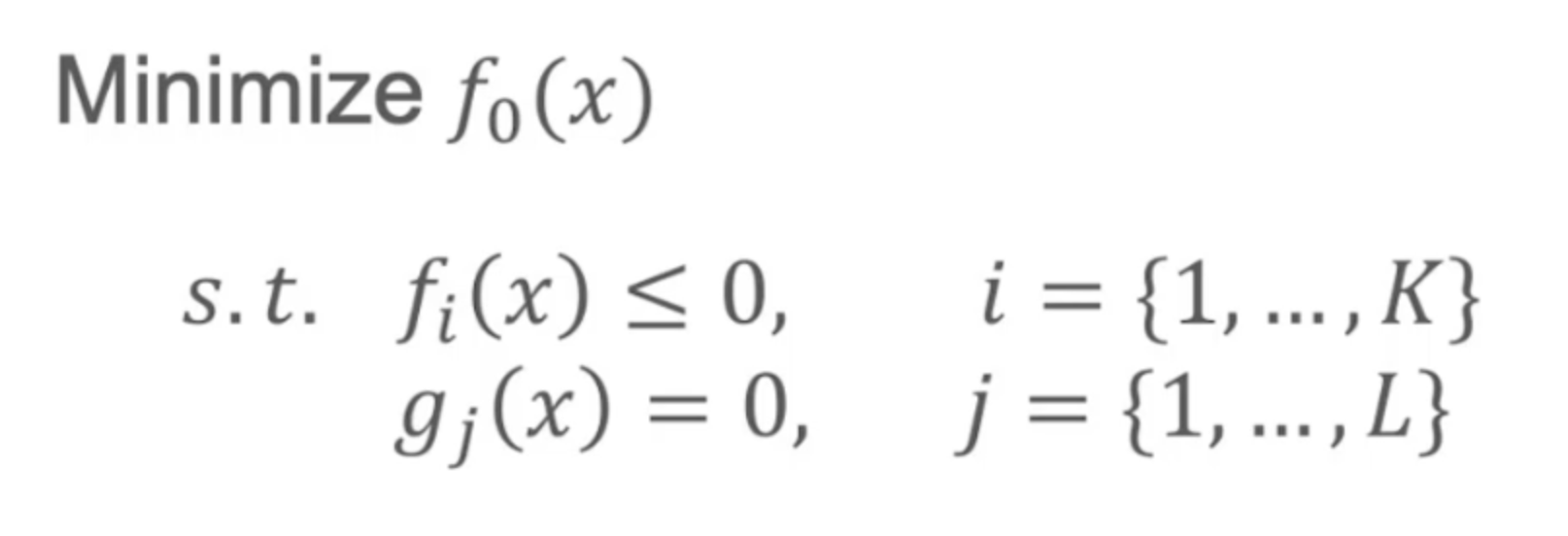
其中s.t.代表这个函数会有的约束条件。我们管x叫做定义域，管f(x)叫做值域，也就是所有可能的取值范围。

再来我们先规定一些定义，在下图中，值域是被x1和x2所约束的，也就是有两个约束条件，那么在这两个约束条件内的区域称为可行域feasible region，也就是这里面 的所有x取值都是满足这个函数的。再来，在这个可行域内的某个点我们叫做可行解feasible solution。在这些可行解中，存在最佳的一个解，叫做最优解optimal solution。

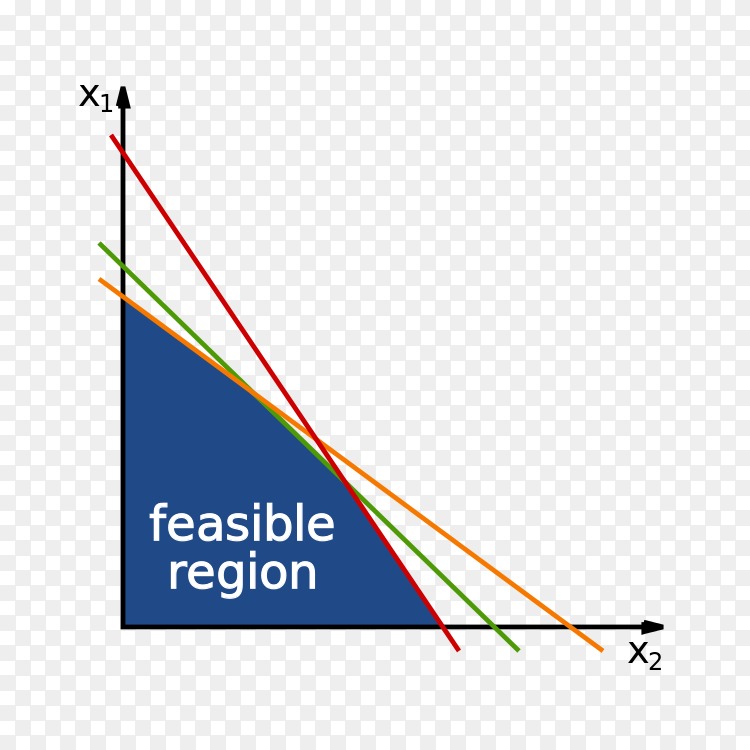
那么在可行域中，我们任选了两个点，如果对于这两个点x，y存在一个alpha值属于[0,1]，我们有 ，则这个集合叫做凸集convex set。则在下图中属于凸集的是(A）

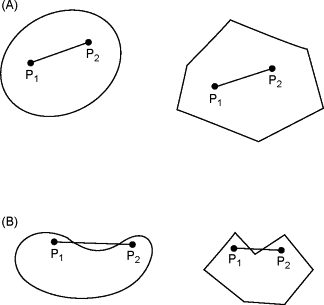
还有一些定理比如两个凸集的交集也是凸集。

什么是凸函数？

凸函数的定义为在该函数的凸集定义域内任意两个点x，y，函数满足 。用人话说，就是函数内任意两个点的连线中的convex combination一定在定义域上convex combination的上方。

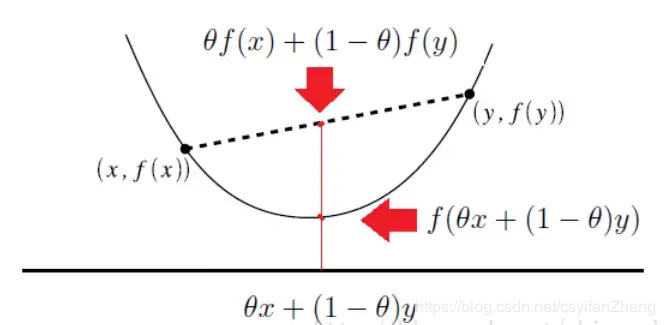
那么我们在拿到一个函数的时候怎么去判断他是不是一个凸函数呢？

• 根据First order convexity condition, 我们首先要求函数f是可导的，并且对于任意的x，y当且仅当满足 时，f为凸函数。
• 根据Second order convexity condition, 我们首先要求函数f是二阶可导的，并且对于任意的x，y当且仅当满足 时，f为凸函数。

常见的凸优化问题比如线性规划，则可以使用很多在线solver可以解决。

那么我们对于一般无约束的最优化问题都很好解决，比如 ，我们只要求出x对于f的导数等于0的时候x的值，和y对于f的导数等于0的时候y的值便能得到整个函数的最小值。可是如果像文章刚开头的凸优化问题标准形式，带有约束条件时，就 会变得棘手，所以如何把带有约束条件的最优化问题转变成无约束条件的最优化问题呢？

拉格朗日对偶

这时候我们就需要引入一个辅助函数，叫广义拉格朗日函数generalized lagrange function，之所以叫广义，就是它并不会对优化问题的函数和约束条件进行某种限定，接受任何形式的约束。

其中x即为原函数中的x值，alpha是一个k维向量，每个alpha对应一个非不等式约束，也就是说对于每一个ci我们都有一个alpha_i。相似的，对于每一个等式约束我们都有一个对应的beta_j。

我们还需要一个辅助函数：

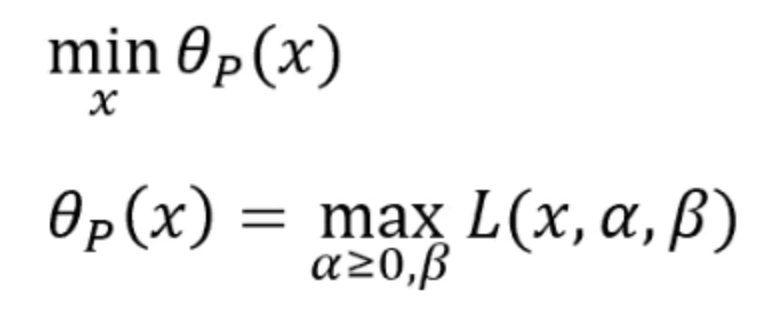
对于任何的x，我们都可以用theta_p函数来求得一个值，这个值我们可以通过确定拉格朗日函数的x值时，求得其最大值。我们称这个问题是最优化问题的原始问题primal problem。因为这两个函数是等价的，之所以我们需要定义这个函数是因为我们尝试把优化问题中的约束条件融合进原始问题这个无约束函数中。故原始问题的解，就等于优化问题的解。

为什么我们可以用原始问题来代替最优化问题的解？

我们分两个部分来讨论，即：

1. 当x满足约束条件的时候：

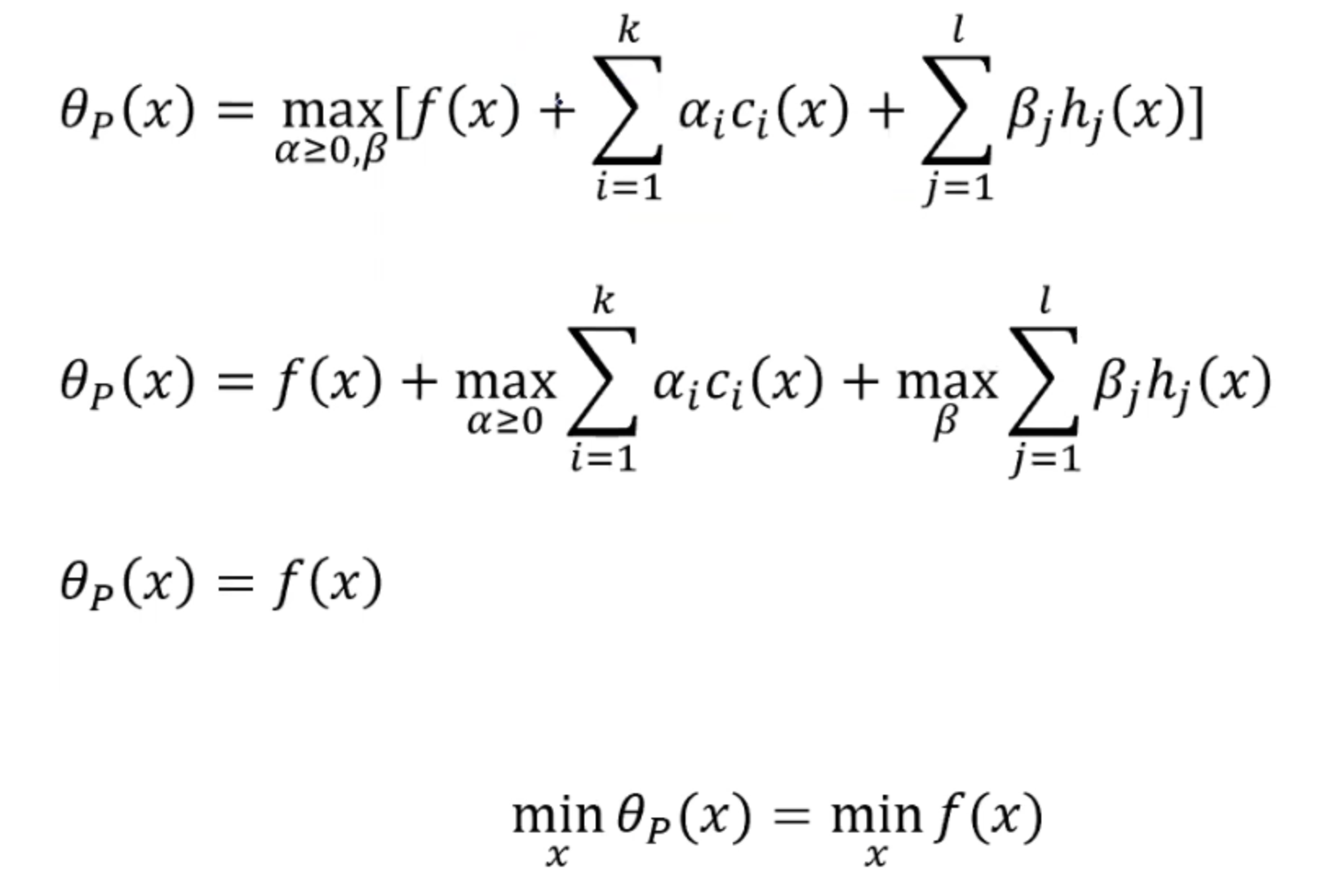
所以当x满足约束条件的时候，即ci都是小于等于0时，alpha都是大于等于0的，所以在第二行的等式中右边的第二项最大就是0。我们也知道hj是等于0的，所以第三项也就等于0。

1. 当x不满足约束条件的时候：

所以当x不满足约束条件的时候，我们的原始问题是趋向于正无穷的。所以无法求得原始问题的最小值。

所以通过以上的推论，我们可以认为如果我们可以找到原始问题的最小值，那么这个值就等价于我们的优化问题。

但是对于怎么去求解这个原始问题的最优解我们还是不知道。那我们可不可以再找到一个对偶函数，让它的值也去等价于原始问题的值以便于更简单的求解原始问题呢？答案是肯定的，所以我们可以定义另一个函数theta_D(x)作为原始问题的互补形式，也就是要求使得拉格朗日函数最小。

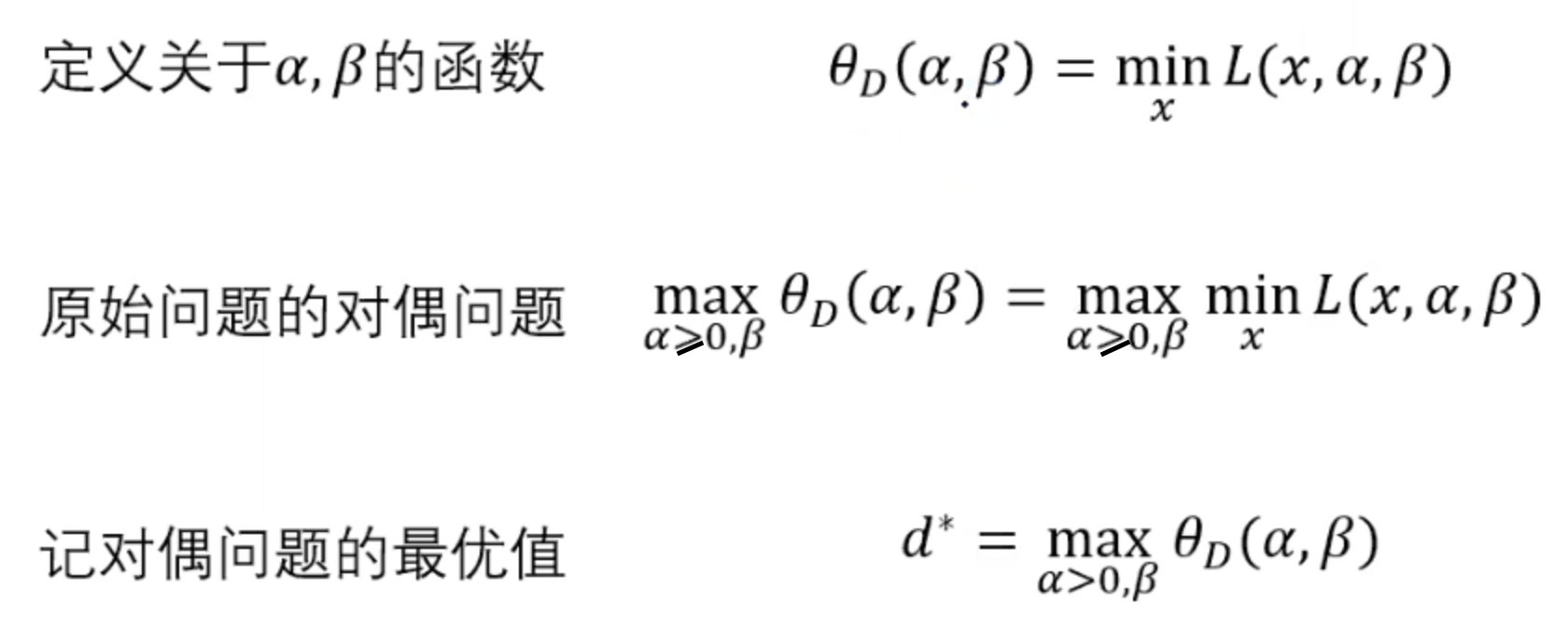
所以我们现在得到了原始问题的对偶问题，那么如果原始问题和对偶问题都有最优解的话，我们管这个不等式叫做弱对偶性:

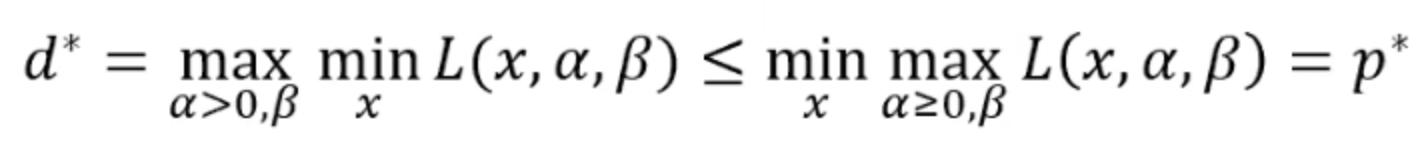
我们肯定不能凭空捏造一个对偶函数，那么我们看看怎么去证明他们的对偶性：

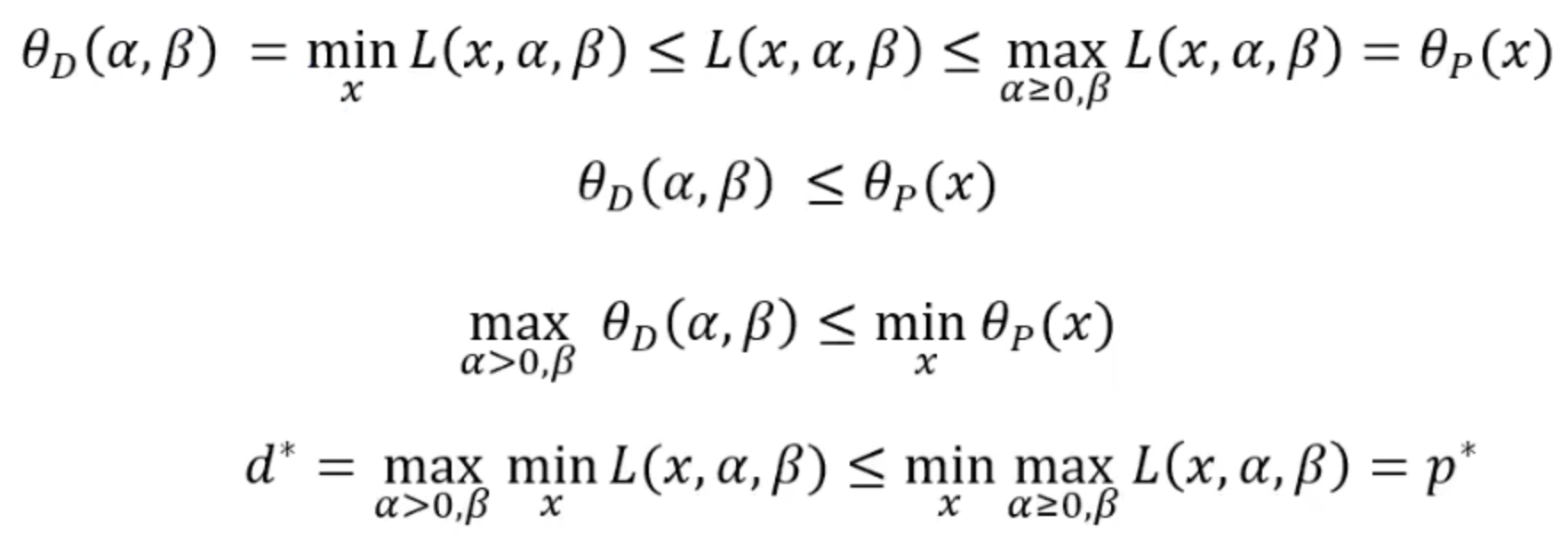
所有我们可以有一个推论，即如果d* 等价于 p* 的时候，那么x和两个拉格朗日乘子同时是原始问题和对偶问题的最优解！

那么在什么情况下d* 才会等价于 p* 呢？

这就要引入一个新的定理叫做Slater条件：

• 定理：对于原始问题和对偶问题，假设函数f(x)和c(x)都是凸函数，并且h(x)是仿射函数（由一阶多项式构成的函数）；并且假设不等式约束c(x)是严格可行的，则存在x，alpha，beta，使得x是原始问题的最优解，alpha和beta是对偶问题的最优解，并且。

当满足了slater条件的时候，我们叫这个等式为强对偶性

那么在满足了强对偶性之后，我们应该怎么解出来最优值呢？KKT条件给了我们一个更加具体的定义，并且告诉我们当满了强对偶性的时候，最优解满足下面的条件：

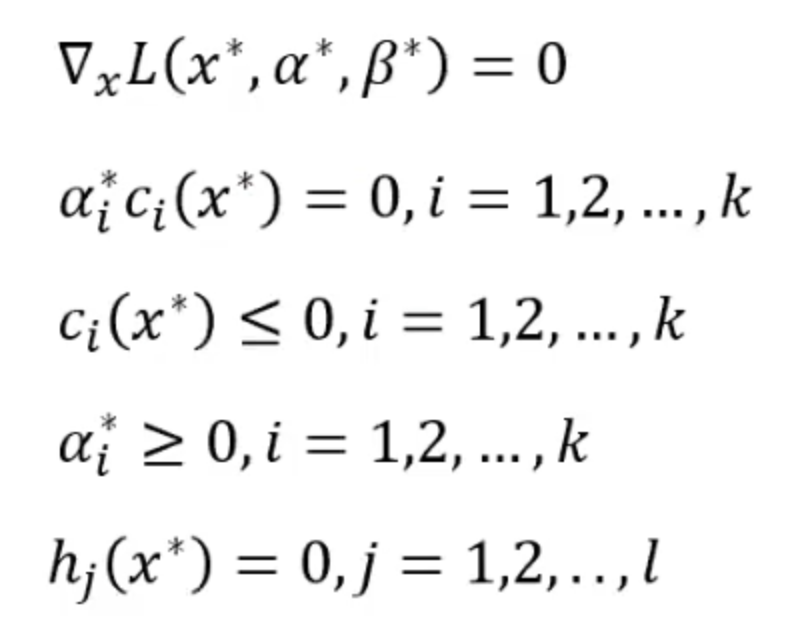
其中第二条乘子和不等式约束相乘是等于0的被称为KKT对偶互补条件。

随后我们便能通过代入KKT条件呢求解出x的取值。

在机器学习中SVM的对偶求解是最著名的，关于怎么把对偶应用到求解SVM中，请转至SVM 的博客中。