宏观理解
GBDT（Gradient Boost Decision Tree）中文叫梯度提升决策树，是一种集成学习中的boosting方法。boosting中除了GBDT还有比如Adaboost，目的在于在不使variance上升的情况下减少模型bias，所以在各大竞赛中都表现优异，在广告系统中也被广泛应用。缺点在于及其容易过拟合所以经常我们使用的时候需要加上正则化。
微观分析
我们知道boosting是由一些弱学习器串联而成，GBDT中用的弱学习器顾名思义就是决策树。我们还可以使用别的弱学习器比如逻辑回归，我们统称为GBM（Gradient Boost Machine）。在GBM中我们需要依靠每一个弱学习器，所以它也是一个加法模型，而不是bagging那样众投。我们把一个加法模型写作：
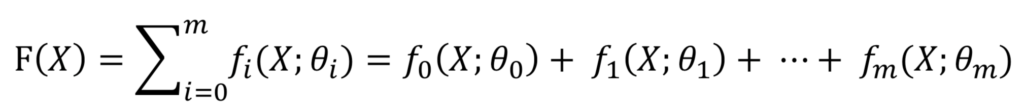
每一个小f代表一个弱学习器，最后相加形成一个boosting模型F(X)。
因为是串联而成，加法中后面的基模型要依赖于前面的基模型，所以我们无法一步完成计算，这时候我们需要前向分步算法来帮助我们。
我们假设有了前面 k个模型的结果，也就是从f1 + f2 + f3 + … + fk我们简写成Fk(X)的值，因为boosting模型是依靠下一个基模型来调整整个模型的损失，所以也就是说我们需要最小化损失函数
。目前为止Fk是已知的，我们需要求解
是多少的时候才能让loss最小化。
这个过程相同于梯度下降法，在梯度下降中如果我们有Loss(θ)，下一轮迭代中我们希望Loss(θ + Δθ)变得比Loss(θ)更小求解Δθ。
那么梯度下降法Δθ = – (∂L / ∂θ) 。在上面的公式中也可以同理，我们要让loss加上变小，
那
就和Δθ一样，我们只要求出：
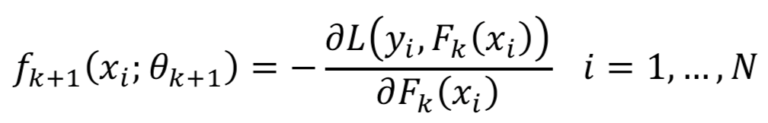
那么如果想求出参数θk+1的值，也就是让每个xi都要近似于- (∂L / ∂Fk(xi))而不再是一开始的label y了。这就是GBM模型的精髓部分，在越往后的模型中我们要拟合的就不再是一开始的标签y而是residual残差。只要我们可以拟合的很好，那么整体的GBM模型的loss就是在下降的。总结一下所有的步骤就是：
- 初始化Y = f0(X)用来计算第一轮的loss
- 在k = 0，1，2，… , n的模型中我们计算出新的需要被拟合的y值
- 数据集变成了
后拟合下一个基模型得到新的预测值y
- 以上步骤迭代最后输出最后的预测值F(X)
以上是GBM模型的训练过程，那么如果我们把每个fk基模型替换成决策树（一般用CART分类与回归树）就是GBDT模型了。
GBDT可以做分类也可以做回归，唯一的区别就是两种任务的loss function不同。对于分类任务我们用logloss也就是交叉熵，对于回归任务我们用MSE。那么我们可以把以上的GBM模型训练过程再细化一些来展示分类和回归问题中的训练过程。
- 对于回归问题：
- 初始化Y = f0(X)为y的均值或者0
- 在k = 0，1，2，… , n的模型中我们计算出新的需要被拟合的y值
- 数据集变成了
- 以上步骤迭代最后输出最后的预测值F(X)
即为MSE求导后的表达式。
- 对于分类问题：
- 初始化
为y的均值的logit函数
或者0
- 在k = 0，1，2，… , n的模型中我们计算出
，并且求解
- 数据集变成了
- 以上步骤迭代最后输出最后的预测值F(X)并且概率为P = sigmoid(F(X))
- 初始化
即为logloss求导后的表达式。因为分类问题是拟合的概率所以才计算残差的时候需要sigmoid来拟合概率。