宏观理解
在机器学习中有很多时候我们需要一个距离的参数。就像求数学中两个坐标点的距离一样,因为数据在分布中本身就是一个坐标点,所以同样需要计算两个数据点的距离。 比如KNN算法我们要找离某一个点最近的k个数据点,再比如FaceNet中计算两张人脸的距离来判别是否是一个人等等。 还有很多别的距离定义,比如汉明距离等。那么怎么求这些距离,区别在哪里?
我想先引入范数(norm)这个概念,它相当于更严谨的距离、长度的定义。 它规定了在多维空间内的向量之间的距离的函数,我们有不同的函数可以用于求出两个向量的距离,他们都可以纳为范数的概念中。
微观分析
L-P范数中的P可以是0、1、2、正无穷,下面这张图可视化的是在三维空间中到原点的范数为1的点构成的图形:
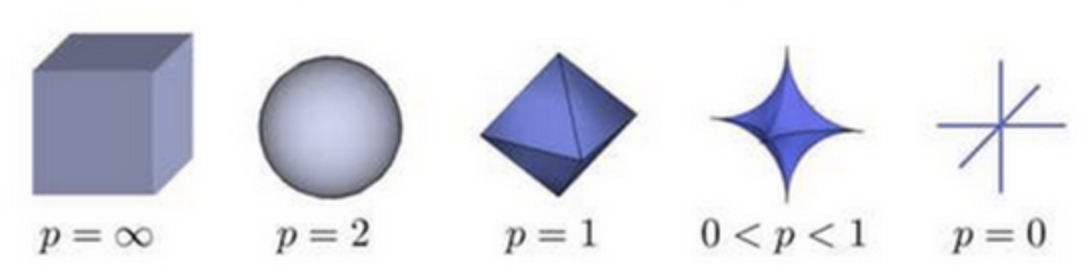
其中P = 2的时候就是欧氏空间二阶范数,也叫欧式距离(Euclidean distance),也是我们在机器学习中应用的最多的一种度量方法,它的计算函数是这样的:
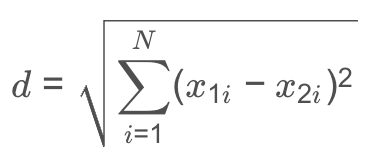
也就是两个点或者两个向量矩阵的差的平方再开根号。
P = 1的时候就是欧氏空间一阶范数,也叫曼哈顿距离(Manhattan Distance)。这个名字来源不是某个发明人而就是纽约的曼哈顿,因为纽约的街道往往横平竖直,就好比把曼哈顿平均给切成了n*n块一样。下面这张图就好比整个曼哈顿,有意思的是从左下角到右上角的这4中颜色的连线,按照曼哈顿距离来计算都是一样的。本人非常建议出租车改成这种计价方式,这也就避免了很多黑心司机给外地人绕道走。
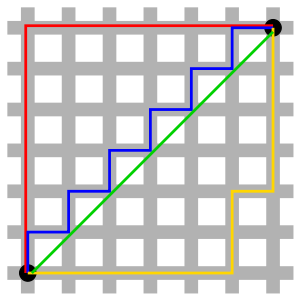
它的距离函数是:
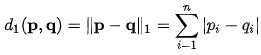
当P等于正无穷的时候,也叫做切比雪夫距离(Chebyshev Distance)主要被用来度量向量元素的最大值,所以计算函数很简单:
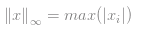
当然我们还剩下当P = 0的时候,这种情况争议很大,并不严格属于范数但是也可以称为广义上的范数。它的公式是这样的:
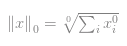
但是问题来了,啥叫0平方?那这么说所有大于0的数字都是1了呗?嗯。再加上开了一个0次方,就很烦,所以我们一般把这个公式改写成计算向量中有多少个非零值:
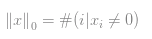
还有闵科夫斯基距离(Minkowski Distance),它与上面几种不同的是它并不是一个范数,而是一组范数,这些组随着p的取值而变化:

如果我们把P = 0, 1, 2和正无穷带入,是不是就变成了以上见过的欧式距离,切比雪夫距离,曼哈顿距离啥的。
我们除了各种范数之外,还有用角度来衡量两点距离的比如说余弦距离,也叫做余弦相似度。它更看重的是因为角度所产生的方向上的距离,公式为:
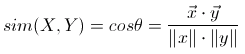
所以即使我们在坐标轴上把其中一个点在延长线上拉长,欧式距离变化,而余弦距离不会变,因为角度并没有改变。
最后说一种耳熟能详的汉明距离(Hamming distance),在信息论中它用于计算两个等长的字符串在每个index的位置上的字符不一样的数量,也可以理解为这两个字符串的相似程度。 比如字符串A = “01122”和字符串B = “02123”的汉明距离就是2。
