宏观理解
L1-Norm 和 L2-Norm(或者叫L1范数和L2范数)是比较常用的两种正则化。所谓正则化是用来防止过拟合的一种手段,换句话说,如果把每一个模型参数都学习的特别好,那么最后这个模型会及其的贴合训练集的数据,测试集稍加变换就会让模型无法适应。为了让模型更好的适应的各种数据集,行话叫加强模型的泛化,我们就强制让一些模型参数不要学的那么好,或者我们可以干脆扔掉一些模型参数。这样虽然会在训练上降低准确率,但是在测试集上却可以提升不少。
虽然人们都说L1-Norm 和 L2-Norm是两种正则化方法,但是为什么要有两种?区别在哪里?他们真的仅仅是用来处理过拟合吗?
微观分析
我们拿线性回归来举例子吧,我们之前见过的线性回归的损失函数是这样的:
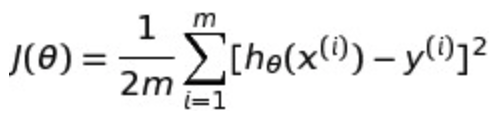
如果我们想在线性回归上加上L1-Norm,也就是我们说的Lasso回归,那损失函数就会变成这样:
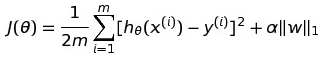
| 后面的α是一个超参数,自己来定义你想要的正则化强度。后面的 | w | 1 就代表的L1-Norm了。L1正则化是指权值向量w中各个元素的绝对值之和,通常表示为 | w | 1。 |
同理我们可以加上L2-Norm,也就是Ridge回归(岭回归)。那损失函数就会变成这样:
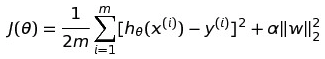
L2正则化是指权值向量w中各个元素的平方和然后再求平方根。
那么我们在损失函数后面加上这玩意会造成什么结果呢?为什么这样就可以防止过拟合呢?
对于L1-Norm:可以产生稀疏矩阵,可以用来防止过拟合,也可以用来特征选择。 对于L2-Norm:用来防止过拟合。 上面说的产生稀疏矩阵,所谓稀疏矩阵也就是在矩阵中的很多元素都是0。这样在线性回归中我们会使得很多参数最后被0给消除掉,这些特征可以被认为对训练模型没有很大的意义,被清除掉也不会太折损准确率,所以在一个特征很多的模型中训练一个稀疏模型可以仅仅保留住那些对模型贡献最大的特征,又达到了防止过拟合的效果。
下面是L1-Norm的可视化:
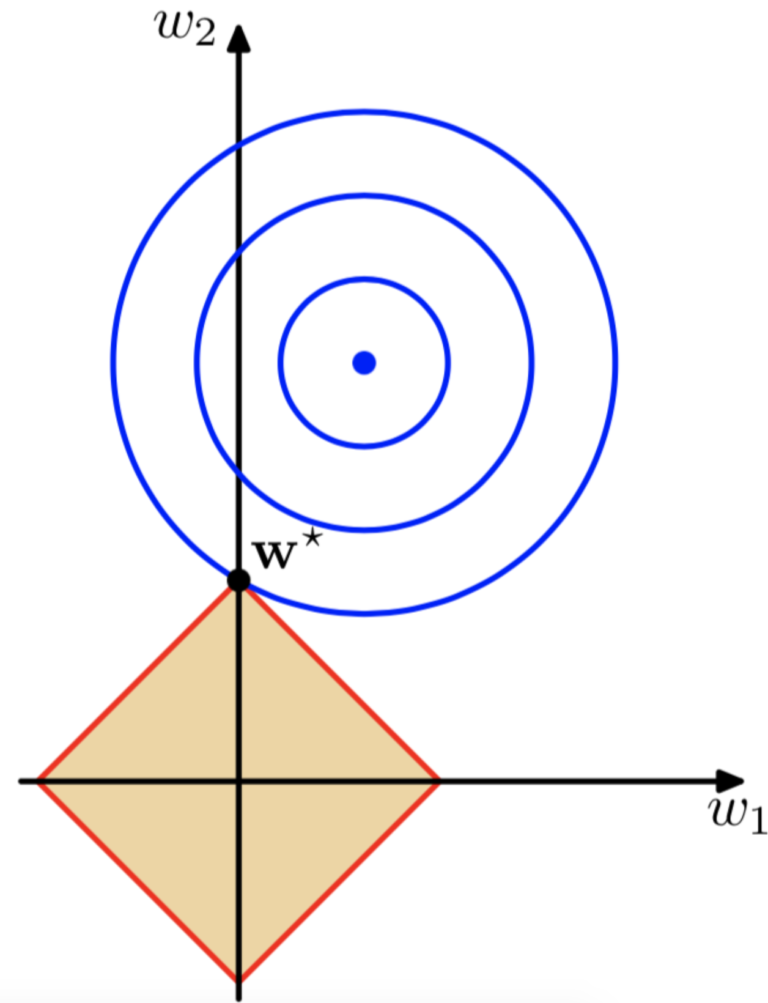
| 我们考虑一个二维特征的情况,那些一圈一圈蓝色的就是损失函数J的等值线,那个有棱角的黄色四方形就是α | w | 1的函数图,他们两个相交的点w*为整个损失函数的最优解,那么在这种情况下,w2的值变成了0 。如果我们可视化出来3,4,5维特征,会发现α | w | 1的函数图是一个具有棱角的多边形,这也就使得和损失函数相交的时候很多特征被置于0 。这也是为什么L1-Norm可以使得矩阵很多参数变0产生稀疏矩阵。 |
同理对于L2-Norm的可视化:
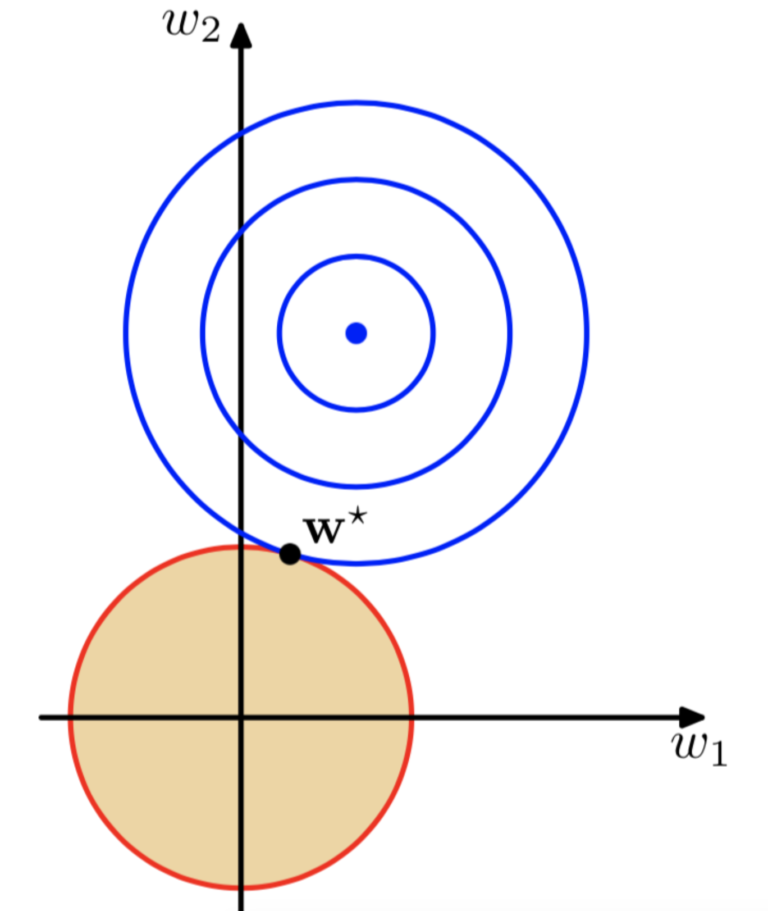
正则项函数变成了一个没有棱角的圆形,所以在相交的时候很少会把参数置于0,往往都是一些很小的很接近于0的数值,所以L2-Norm并不能产生稀疏模型。
至于为什么L2-Norm会产生很多接近于0的值,那么就要看梯度下降的时候做了什么,在梯度下降中我们把带有正则项的损失函数求导可以得到:
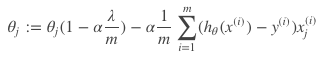
可见每次因为正则项的偏导我们都要乘以一个小于1的数字,这样一轮一轮下去就会变得越来越小。
对于我们之前见到的正则化系数α(即图中 λ):
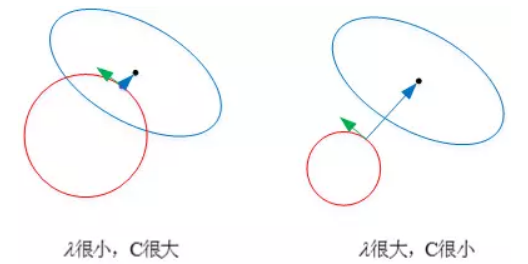
如果它很小就代表正则化强度小,我们见到过的正则项函数图形就会很大,就会离最优解越来越近。
相反它很大就代表正则化强度大,我们见到过的正则项函数图形就会缩小,就会离最优解越来越远。
