宏观理解
我们之前说过的算法都是人脸检测,比如Faster R-CNN和MTCNN。可以在一张图片中找出人脸的位置,但是我们常见的人脸识别系统并不能只依赖于人脸检测,我们还需要一个步骤就是人脸识别。
人脸识别大致有两种,第一种是给出一张人脸来对比是否和另一张一样,第二种是给出一张人脸来判断是否在一个数据库里。这样我们把人脸检测和识别的算法结合在一起就是一个完整的人脸识别系统了,这个流程类似这样:
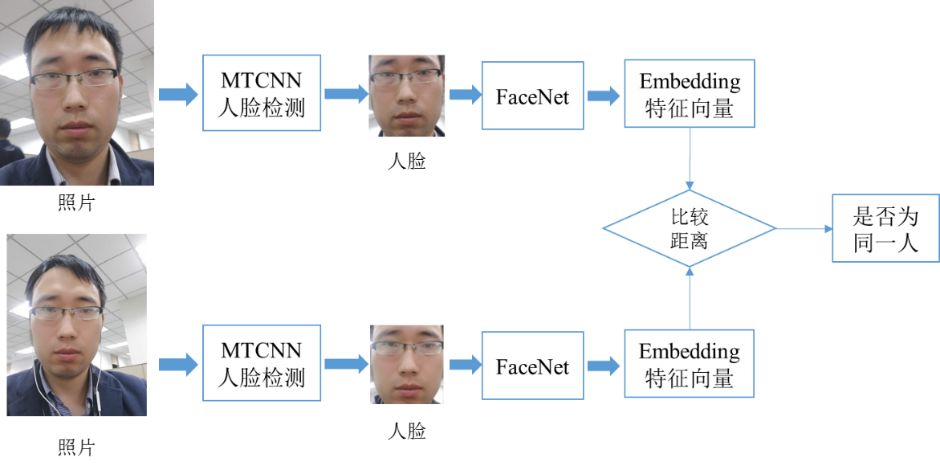
现在我们就介绍一种可以识别的算法FaceNet。FaceNet的作用在于给出两张照片,它用欧式距离来判断这两张照片的人是不是同一个人。比如下面这个图中,我们规定两张照片的欧式距离小于1.05的判断为同一个人,所以左右都为同一个人但是上下都大于1.05判断为不同的两个人。

其实是一个很简单的过程,先把人脸embedding然后计算两个编码的欧式距离就好,那么这篇论文贡献的就是一个新的loss function来使相同的人脸距离越来越近,不同的越来越远。
(注:那么为什么要用欧式距离而不是用cos距离来做呢?因为如果用cos的话进行N:N的比对需要O^2的复杂度,但是如果用欧式距离的KD-TREE之类的数据结构可以很大的提高效率。)
微观分析
这种新颖的loss叫triplet loss。我们先随机拿出一张照片叫anchor。然后我们再随机从标注好的同一个人的照片中再拿出一个叫positive(可能翻译成正样本?),最后从不是同一个人脸的数据中随机拿一个叫做negative(就叫负样本吧)。然后这三张照片通过embedding之后,交给triplet loss计算出一个损失。整个过程就是这样的。
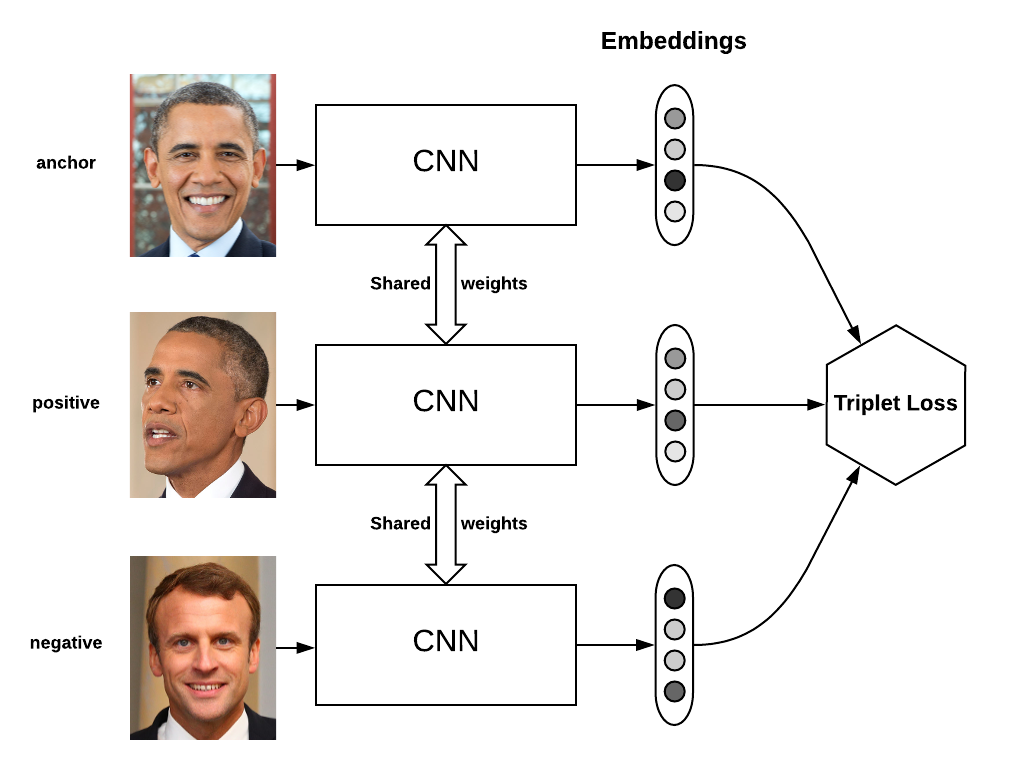
这个损失在优化完我们当然希望anchor和positive的距离越来越近,anchor和negative的距离越来越远。所以我们的目标就像这张图:
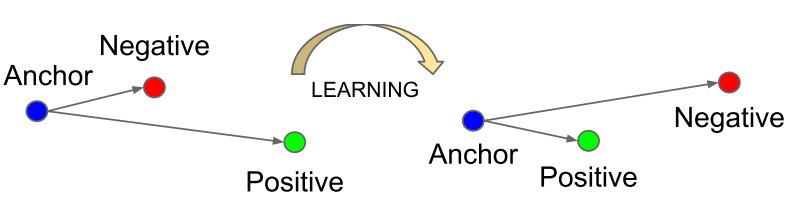
| 为了更好的应用,我们还可以在这个loss上加上一个超参数α当作margin,就像SVM一样,不仅要找出一个答案,我们还要这个答案变得尽量最好。我们定义一下anchor为A,negative为N, positive为P。所以我们写成 | F(A) – F(P) | + α < | F(A) – F(N) | 。F我们可以理解为embedding的函数。这样在训练完可以让我们的算法更加有鲁棒性。 |
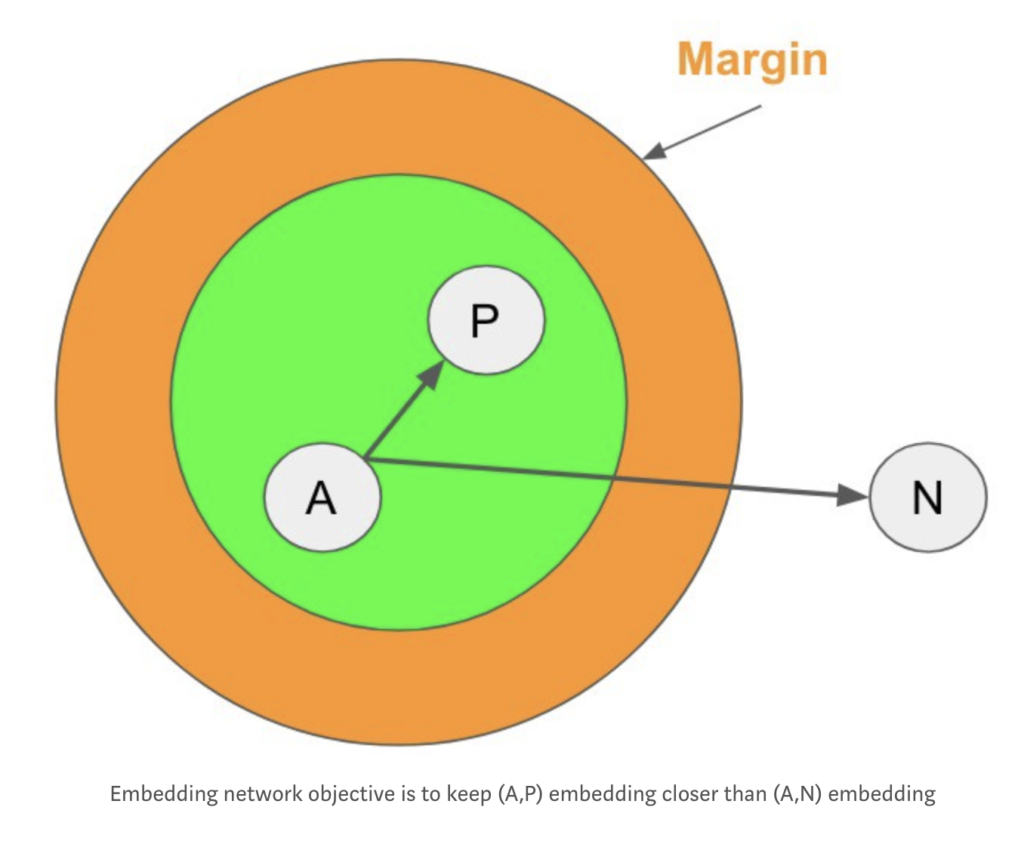
| 现在我们稍微移项一下就有了我们的loss = | F(A) – F(P) | – | F(A) – F(N) | + α |
| 在训练过程中,因为每个样本都是由一个三元组组成的,如果我们把数据集中的所有三元组都先找出来再全部来做loss,这样的复杂度异常的高。所以我们选择在每次的一个batch中,寻找有哪些组合是满足 | F(A) – F(P) | + α < | F(A) – F(N) | 的,然后仅仅求出这些的loss进行反向传播。但是还有一个问题就是,为了更加的优化这个过程,即使在一个batch中也能选出很多种三元组,那么优化就落在了怎么选择这些三元组的问题上。我们可以把每个batch的数据平均一下,来保证每个batch中有P个人,每个人有K张图。接下来有两种方法来选择: |
- 全生成:单纯的选择所有满足的三元组,也就是PK(K – 1)(PK – K)种选择。但是有很多对训练并没有帮助的简单三元组。
- Hard样本生成:在所有的样本中找出离他最近的反例和离他最近的正例,也就是PK种选择。但是生成算法复杂度太高,并且很容易受到异常值对训练的干扰。
| 但是基于全生成和hard样本生成的缺点,我们都觉得这就是两个极端呀,那么我们干脆中和一下吧,所以我们最终在实践中会先找出所有的(anchor,positive)组合,然后再随机找一个满足条件( | F(A) – F(P) | + α < | F(A) – F(N) | )的negative样本,不追求于hard样本。 |
最终这个算法的流程就是这样的:

在embedding之前还有一个L2 Norm,它的意义在于把之前的数据归一化了之后,数据就可以用欧式距离来度量了。其次因为我们之前有一个margin,如果不归一化的话,会对选取margin带来很大的影响。
