宏观理解
PCA(主成分分析)是一个降维算法。因为很多数据集大维度很大,比如说下图7个数据点每个数据点有30个特征,这种维度的数据先不说里面混杂着很多无关特征,如果直接拿来train,他会使模型变的很复杂,如果想改善我们要增加很多训练样本,训练时间也就相应增加许多。那么pca可以帮助我们在仅有的7个样本中,把每个样本的维度从30缩小到2(当然这个图降到2有点过分了,但是很极端的说明了作用。。),这样7*2的训练集就很漂亮。在降维的过程中pca一个很关键的原则就是,你给我2维的特征里面的信息量必须和30维的特征里面的信息量尽量一致。
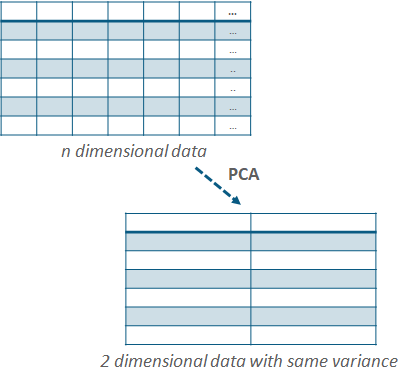
微观分析
PCA的降维原理就是把原先的n个特征用数量更少的m个特征取代,这m个新特征是旧特征的线性组合,这些线性组合最大化样本方差,尽量使新的m个特征互不相关。
最大化样本方差和特征互不相关如果用数学表示出来就是用方差variance和协方差cov的计算公式:
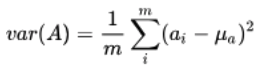
这里就不详细说什么是方差和协方差了。
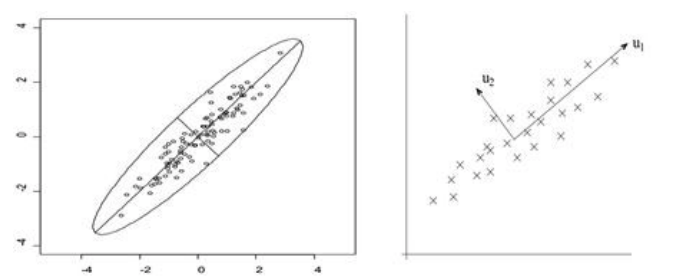
假设我们有左边的数据集带有两个特征,其中长的45度斜线为主要线性分量,短的45度斜线为次要线性分量。如果我们把右图想像成一个坐标轴,横轴为特征u1竖轴为特征u2 。那么所有的x样数据点都可以线性的表示出来,比如数据点X = aU1 + bU2。
因为我们要减小特征数量,u2的信息量远小于u1,所以我们删掉u2以保证保留下来的信息越大越好。
如果我们要最大化样本方差,就是要最大化(我们已经把u2删掉了):
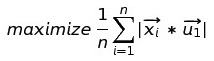
我们把上面的式子写成方差的计算公式即:
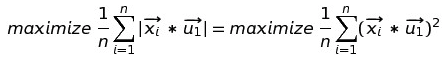
接下来我们推导出来最大化方差的公式:
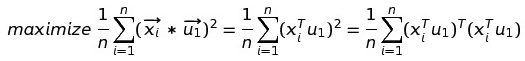
其中是我们把特征矩阵点乘,假设我们把第一个X的数值叫做a,把第二个X的转置的数值叫做b,那么我就有了如下的矩阵:
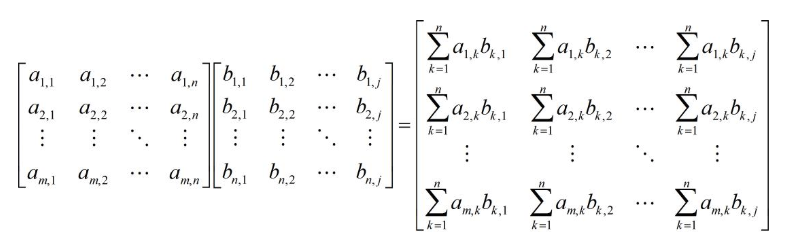
其中a1,1和b1,1都是相等的依此类推。所以在最后的矩阵中,我们管它叫协方差矩阵,对角线上都是两个相同的值相乘。想象不出来的同学给你们举个例子:
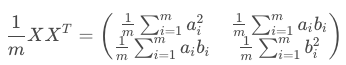
所以我们要做的就是找到一个u1矩阵的值,使得协方差矩阵中对角线(方差)最大化,除了对角线的其余值(协方差)最小化也就是全部为0 。
为了我们要达到的目的PCA做的基本步骤如下,假设我们有数据集 X:
- 首先计算X中每一行Xi的平均值Xi_mean
- 我们用Xi整体减去平均值Xi_mean得到新的矩阵X_new
- 我们计算出新的矩阵X_new的协方差
- 计算特征值(eigen-value)和特征向量(eigen-vector)
- 把特征值排序,选取最大的前k个(k = 降到多少维)
- 将选出来的k个特征值组成另一个对角线矩阵W ∈ n*k
- 计算出X_new * W即为我们降维后的特征矩阵
我们带一个例子把上述过程走一遍(实例来自hustqb):

