宏观理解
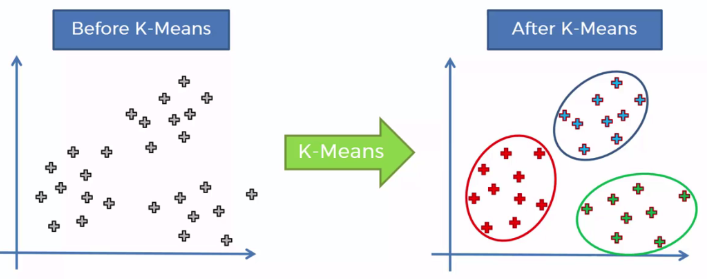
K-means是一个聚类算法,属于非监督学习。当你有一堆数据点,但是没有label,就可以试试k-means来分类。效果就像下面这张图。
这就涉及到一些疑问,比如你让我做聚类,就给我一堆点,我哪知道一共要聚几类呢?上面的图肉眼能看出来大致有3类,那如果我们数据点是下图左边这样呢?你说3类也行,2类也很像,4类也不是不可以。
微观分析
聚类算法大致分为两类:
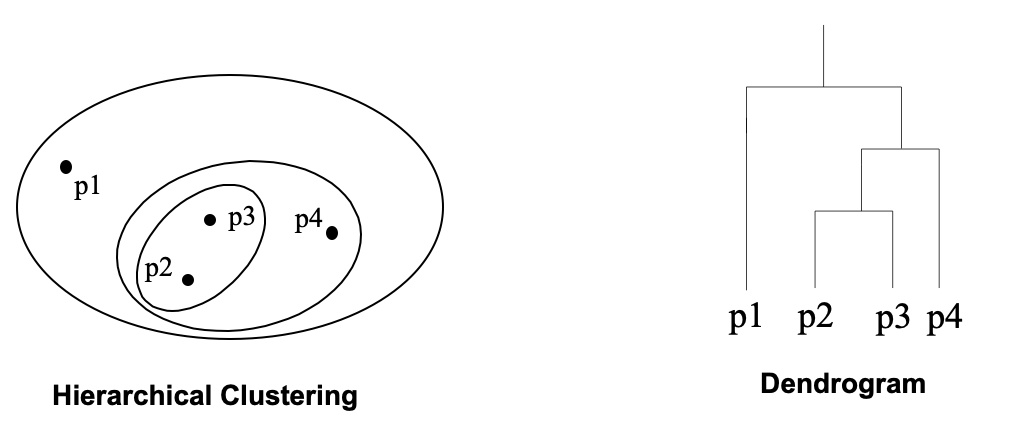
Partition-based clustering – 比如我们要讨论的k-means Hierarchical clustering – 指的是用一个等级树(hierarchical tree)把一个object分成嵌套的类别,或者系统树图(dendrogram)。比如下图这样。
我们这里只讨论最常用的Partition-based clustering。
在基于划分的聚类中每一个类可以用两种方法来表示:
centroid – 指的是在这个聚类中的所有点的平均值(数值) medoid – 指的是在这个聚类中最能代表这个簇的点(某一个点) k-means是通过第一种,质心(centroid)不断的调整而最终分化结束的模型。这个质心也就是我们要分的k类的中心点,也可以叫重心
假设我们有一些数据要分成3份,那么也就是我们需要三个质心。幸运的是我们可以随机找3个点来当作质心,有一些论文讨论过随机选取质心会影响后面的聚类结果但是暂且先不考虑,我们最后会再翻过来看怎么选择质心更好。
好。首先我们现在随机的选择3个质心。接着,我们可以求出来其余所有点对于这三个质心的距离,我们把数据点和他离得最近的质心划为一簇,这样经过这一步,所有的点现在都应该有了一个簇。
接下来我们怎么评估目前为止的聚类好坏程度呢。通过一个叫SSE的objective function。
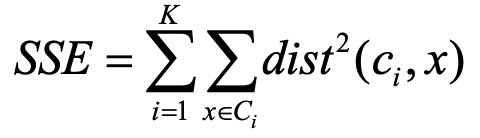
其中,x是在簇Ci里面的一个点,ci是这个Ci簇的mean,也就是质心。这里的dist我们可以用Euclidean distance,当然也可以换成别的。
现在我们所有的点都有了一个簇,每个簇还都有了一个质心,那么现在我们该尝试去更新这个质心了。通过加和同一个簇里的点,然后取一个mean来得到属于这个簇新的质心。然后再把所有数据点和他离得最近的质心划为一类。重复这个过程。算法很简单,下面是伪代码:

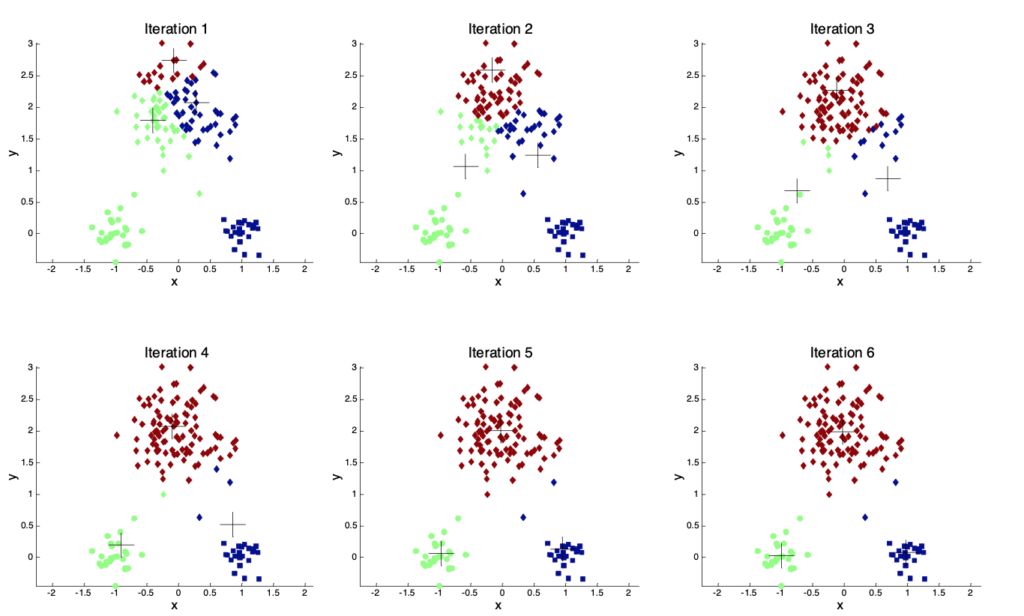
下面我们来看一个图例,从第一轮随机选择3个质心划分直到质心不再变化的过程:
可是因为是随机的选取,所以这个聚类结果并不唯一,比如我们再次随机一遍质心就可能变成这样:
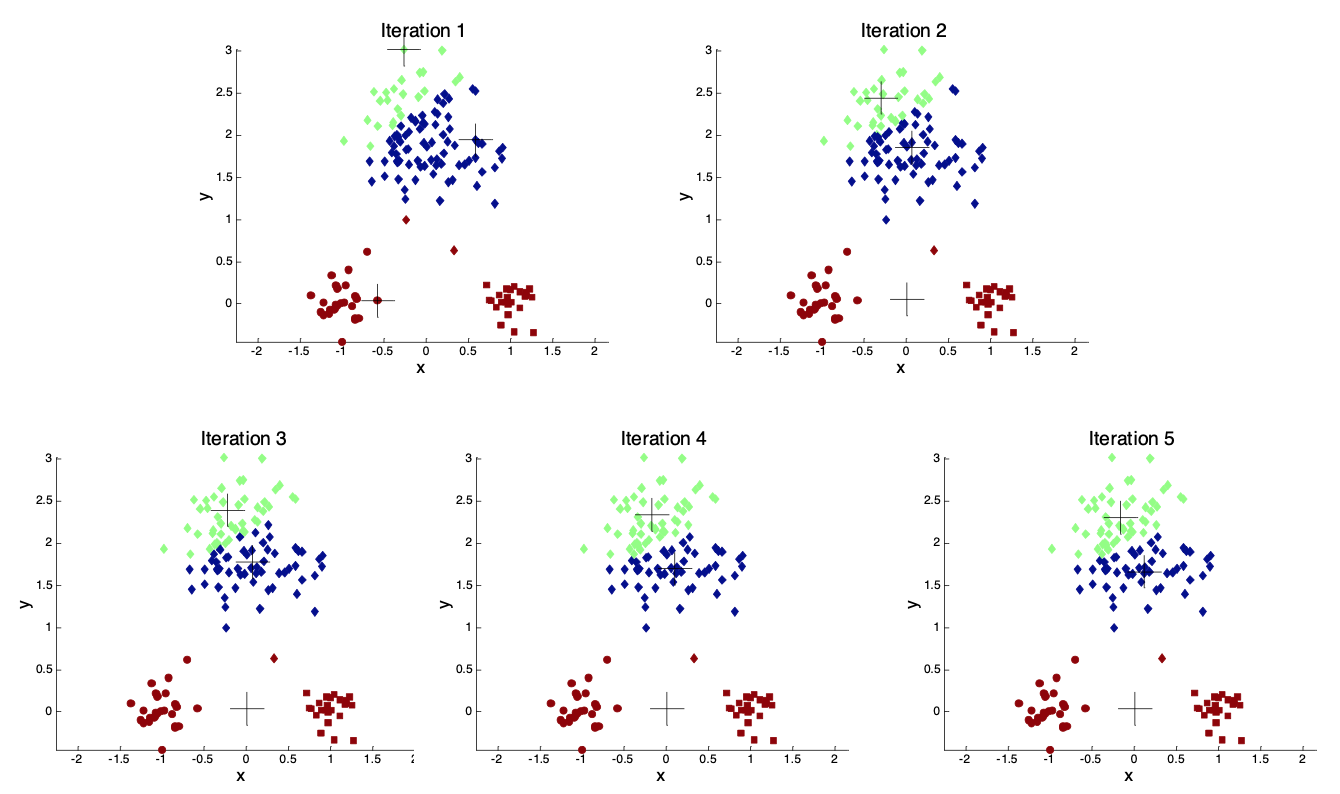
这很不好,及其影响结果。那么通常我们可以尝试下面的方法来更好的初始化质心:
- 多次随机,找最好的SSE的聚类
- 从全部的数据点计算整个数据集的质心,然后依次找离已经选取的质心最远的点。(这种方法需要注意不要选到离群点)
- 二分k均值法(Bisecting K-means),首先将所有点作为一个簇,然后将该簇一分为二。之后选择能最大限度降低聚类代价函数(也就是误差平方和)的簇划分为两个簇。以此进行下去,直到簇的数目等于用户给定的数目k为止。
那么除了初始化质心这个问题,我们还会面临一个问题是在不给定几个簇的情况下,怎么给定k的值呢?
通常我们是循环所有的k取值范围,然后用SSE来评价,最终选取最好的那个,比如下图中当k = 10的时候基本SSE就收敛了,不会再有大的变化,所以我们就可以把k设置为10 。
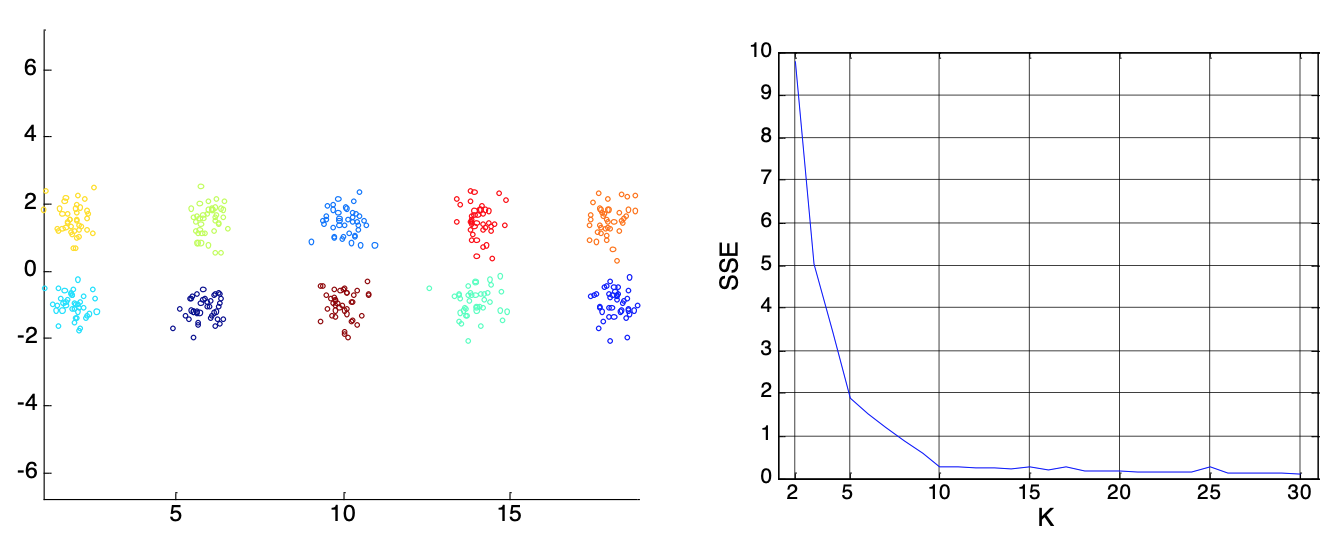
总结一下,k-means的好处是简单易实现,而且时间复杂度不高。
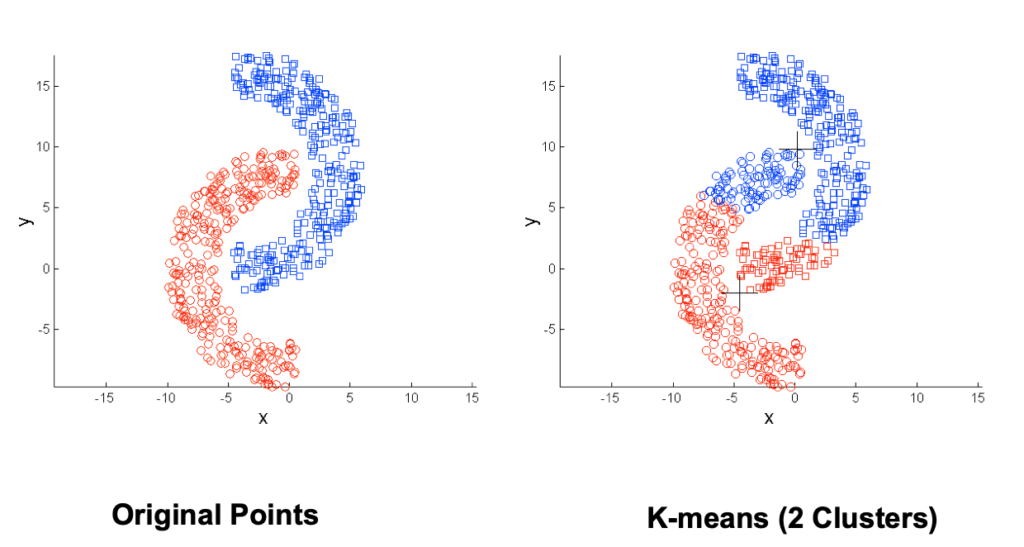
缺点是不能使用在nominal的数据上(可以用k-medoids);对于离群点和噪声比较敏感,万一把离群点选取为质心就更糟糕了;对于选取k值和初始化的质心很麻烦;并且对于一些奇葩形状的数据集效果很差,比如下图。