宏观理解

集成学习是个大杀器，现在几乎所有竞赛的冠军题解都用到了集成学习，甚至到了深度学习中，集成学习也会提高我们几个百分点的准确率。所谓集成学习，就是三个臭皮匠顶一个诸葛亮。我们之前一直都是只训练一个模型，就好像你拿着你不会的选择题去问同学，人家告诉你选A你就写了A，结果老师看完说答案是B，你怪谁？你肯定心想如果当初多问几个人就好了。这就是集成学习的思想，我们为什么要单纯的相信一个模型的结果？我们可不可以同时来训练3个甚至3+个模型然后让他们投票表决这道题选啥，哪个选项支持率高我就选哪个。这个思想就是集成学习中的bagging（Boostrap aggregating），它是很多个模型排排坐每个人举手表决。再比如一个同学告诉你这道题选A，你带着人家的答案去问别人这道题是不是A?也许第二个同学说不对，这个应该是C，因为xxxx的原因不可能是A。然后你又去问第三个同学，这道题张三告诉我是A，赵四告诉我是B，你觉得呢？王五说你看啊他俩都没有考虑到xxxx情况所以应该是B。嗯好。我们离真相越来越近而且每次都有理有据的否定了之前的答案。这个思路在集成学习中叫做Boosting，它是一堆模型串成串，一个接着一个。通过这种思想，你犯错误的几率是不是逐步降低了？

微观分析

我们都知道机器学习中有两个冤家，有你没我那种。他们俩就是偏差bias和方差variance。在一个模型中，如果他的bias很小，那么他的variance一定很大。bias我们可以理解为在训练集上的错误率，variance可以理解为在测试集上的泛化能力。可想而知，如果这个模型在训练集上表现的特别好，overfitting的那种好，那么他的bias一定很低。但是我们都知道overfitting的话在测试集上一定不好，也就是这个模型的泛化能力很差，就是方差variance很大。反过来也一样。所以这俩冤家一直都是不是你死就是我活。

Bagging

但是集成学习可以帮助我们尽量的去协调好这俩冤家，在bias不高的情况下，也不让variance升高。

这就是bagging的功劳，它是一种单个模型有放回采样思想，那么如果有多个模型在同一个数据集里有放回的采样，就是bagging了。

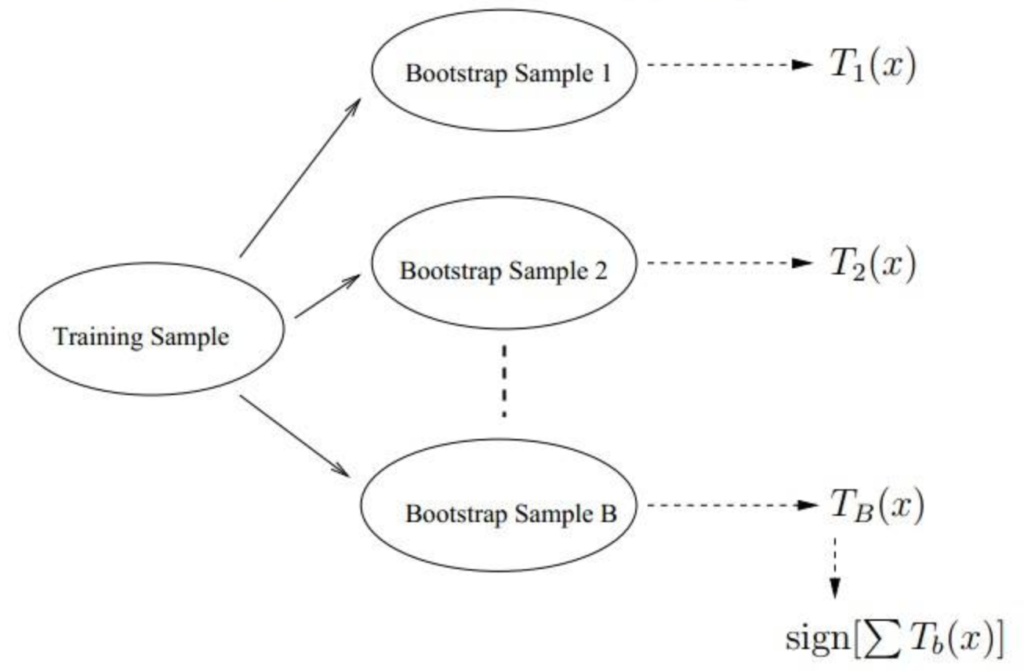
上图就是一个bagging流程，我们有同一个数据集training sample，然后我们有很多个bootstrap的模型，每一个模型都预测了一个值，最后我们进行投票表决。

因为我们之前说了，bootstrap可以在bias不高的情况下，也不让variance升高，那么bagging里面的子模型选择那些本来就可以使bias很低的模型最好，这样既保障了bias不高，bootstrap也保障了不让variance升高。比如决策树。所以我们最常听到的一个bagging模型就是随机森林（Random Forest）了 。

随机森林的大致过程如下：

1. 随机抽取数据，也就是随机采样
2. 随机从抽取的数据中抽取特征：

   1. 随机抽取出特征子集
   2. 选取最佳的划分特征，比如年龄。这就和决策树的过程一样了
   3. 利用年龄划分sub_data_1
   4. 。。。重复以上3步直到结束 在第2步抽取特征的时候，这个数量是我们可以自己设定的。通过公认的经验，总结而出对于分类问题采样特征个数 = floor(sqrt(特征总数))；对于回归问题采样特征个数 = floor(特征总数/3)。

Boosting

我们讲的bagging模型可以在bias不高的情况下，也不让variance升高。那么对应的我们也有在variance不高的情况下，不让bias升高。这就是另一种集成方法叫做boosting。所以如果我们要用boosting，基模型最好选择那些bias很高，但是variance很低的模型。

我们熟知的一种boosting模型就是Adaboost。

在Adaboost中每个基模型具有权重，如果这么基模型的能力越好，那么权重就越大。同样的数据点也具有权重，但是相反，越分不清的点，权重越大。所以Adaboost的学习过程就是在不断更新训练集数据权重和基模型权重的过程。

总结adaboost的过程如下（图来自ScorpioLu）：

值得提醒的是adaboost中的标签为-1 / 1。

最后通过随机森林和adaboost算法，我们可以总结一下两大集成学习的区别：