宏观理解
神经网络感觉人人都知道的感觉。它是个仿生学的模型,仿的就是我们的大脑神经网。我们的大脑神经是由一个一个神经元组成的,一旦有冲动神经元之间就会传递这种冲动, 从起点传输到终点然后我们会接收到信号,做出相应的反射动作。人工神经网络就是模仿了这一种信号传递的过程,就好比我们眼前看到的是一个木板四条腿没有脑袋没有嘴,通过视觉神经传输到大脑皮层的神经网,最后成像告诉大脑哦这货看到一张桌子。过程就像这张图:
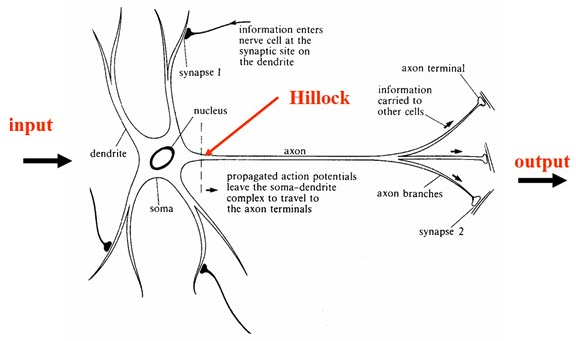
我们也可以让人工神经网络接收一些东西比如一个特征矩阵,一张图片,一段声波,一连串单词,最后来告诉我这是个啥?这项技术其实从19世纪就有了,后来因为技术不成熟被人遗忘,但是从90年代开始突飞猛进一下超过了很多别的机器学习模型,又在2012年因为ImageNet竞赛秒杀所有模型掀起神经网络的热潮。
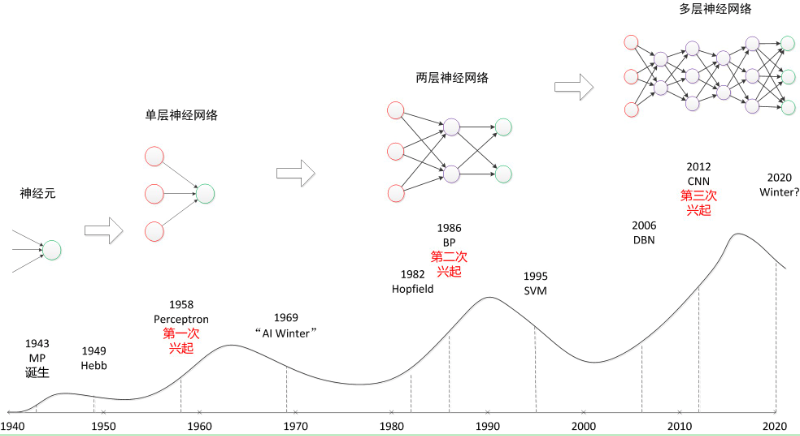
直到今天很多衍生物比如CNN, RNN的诞生更是加剧了人们对神经网络的兴趣。一个人类还摸不到底的模型,不多说了看细节吧。
微观分析
我们先说2层的神经网络,一般说几层,指的是有多少层包含权重,两层的神经网络就是这样的:
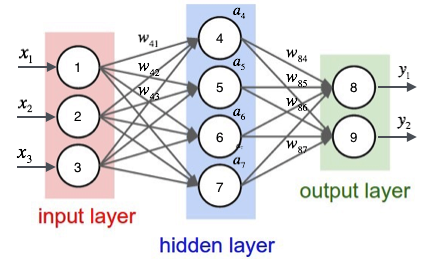
仅有隐含层(hidden layer)和输出层(output layer)有权重,所以我们叫它两层神经网络。输入层的每个x1,x2,x3是我们的features输入,通过中间隐含层的去线性化,然后通过两层权重(weight,即图中w)最后得到答案。如果是二分类问题,输出层可能只有一个node用来表示y = 1的概率,如果我们用sigmoid激活函数就是这样。多分类问题就比其他模型简单了,最后一层的激活函数换成softmax就好,比如上图我们想像成一个2分类的softmax函数。
激活函数的目的就是去线性化,我们知道逻辑回归是一个广义线性模型,如果我们的神经网络用的都是sigmoid当激活函数就好比把很多逻辑回归拼凑一起,它反而不是线性的了。
我们知道输入层就是我们所有的features,输出层就是每个分类的概率,那么中间的隐含层做了什么呢?
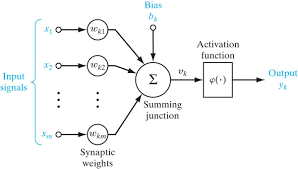
现在我们只看隐含层其中一个node。我们一样有很多的input features,比如年龄身高体重是否结婚。然后我们把左右的input feature x和我们到下一层的权重weight相乘再sum,注意我们sum node上面还有个bias b,这个叫偏置,他的作用是用来拟合更多的情况,想想我们的逻辑回归是不是就是有一个偏置b来让函数可以不止是通过原点来拟合,这里也一样。我们用z来代表这个过程就是。因为是矩阵点乘所以w要transpose一下。接着我们有了z的值,就是要过一个激活函数(activation function)了。试想如果没有激活函数是不是就是线性回归?那就丧失了神经网络的巨大潜能。比如这里我们用sigmoid( σ)函数当作激活函数,通过激活函数我们得到a = σ(z),那么这个a就是我们的y,也就是预测结果。
所以在每个hidden node中,包含的都是两部分,先找到z,也就是上一层的输入乘以这一层的权重再加上偏置b。再把z通过激活函数去线性化,得到预测值y。多层的神经网络无非就是反复这个过程。
现在我们说一下每个参数的维度,这是一个在神经网络中一不小心就会犯的错误。下面是一个3层神经网络:
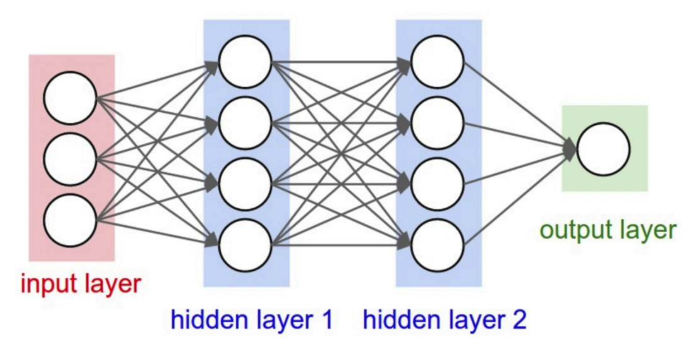
input layer我们有3个node,第一层隐含层有4个node,第二层也一样,最后输出层有一个node输出。我们把每层中node个数记作n。用 “l” 来表示第几层,比如input是第0层,hidden layer 1是第1层依此类推。一个神经网络一共包含的参数有:权重w,偏置b,前一层输出a,和当前层输出σ(z)的z。
所以每层神经网络做的事情就是计算。如果我们向量化的考虑大小,应该是这样的:
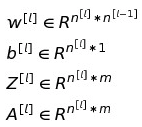
用文字表达:
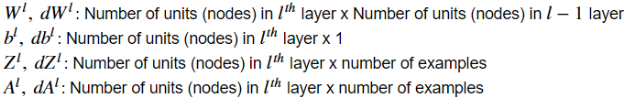
dW,db,dZ,dA是反向传播时候的导数,只是求偏导,大小不变。
比如说我们的hidden layer 1,l = 1,那么w1维度是当前层的node个数*前一层的node个数也就是4 * 3; b1的维度是当前层个数 * 1也就是4 * 1;z和a一样都是4 * feature的个数3也就是4 * 3。
-
Forward propagation 前向传播的过程就像冲动从接受信号往大脑皮层传播的过程。也就是从有了features的输入一直到有一个prediction y。基本过程就跟之前讲的
一样。a就是前一层的输出,σ(z)就是这一层的输出,然后把σ(z)当作前一层输出a再传播给下一层。直到我们有了一个预测值y。这就是一整个前向传播过程。
-
Backward propagation 反向传播的过程就是从原路返回,我们已经有了一个y,那就从y开始求偏导数一直求到input。反向传播是学习神经网络的重点也是难点,所以我会介绍的尽可能详细。
讲反向传播之前我们先看一个简单的例子:
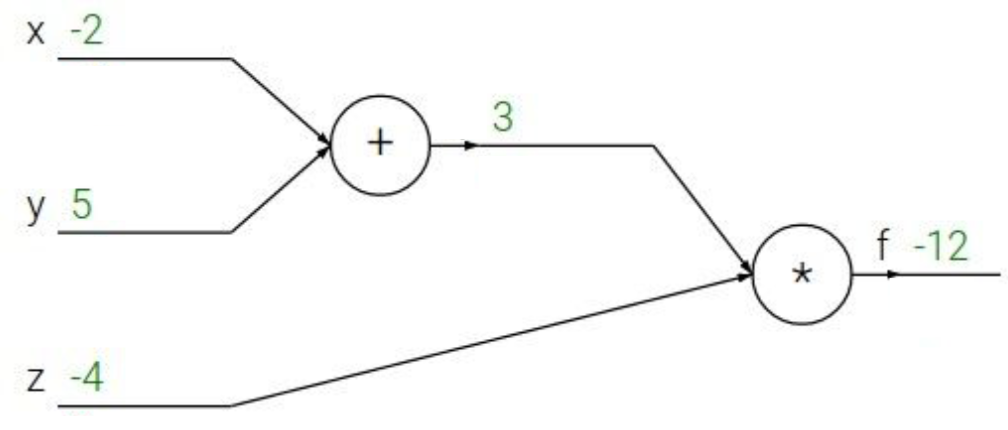
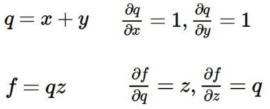
在这个计算图中,我们要计算 f (x, y, z) = (x + y) * z。已知x = -2,y = 5,z = -4。根据计算图我们先相加 x + y = 3 我们假设把这个中间值叫做q = 3。然后q再乘以z等于-12。这个过程就好像我们的前向传播,从已知的x,y,再通过一个激活函数也就是乘以-4最后得到预测值-12。
重点来了,我们要求这个计算图的反向偏导。从f开始:f对于f的导数是1;f对于z的导数是q,也就是3;f对于q的导数是z,也就是-4;f对于y的导数我们用chain rule来计算就是-4 * 1 = -4。同理求出来f对x的导数是-4。
为什么要求偏导?反向传播的意义在哪?想一想,在上图中,f对于q的偏导是-4,说明了什么?是不是说明q对f的影响是消极的,每当q增加h,f的值就会减少4h。f对于z的偏导是3,说明z对f有积极影响,z每增加h,f就会增加3h。同理对于x和y。
在反向传播中,我们首先要对前向传播的预测值求一个loss,把这个loss一步一步往回传。那么反向传播的意义在哪?是不是就是要改变所有的weight和bias来减小loss值。通过什么来减小?就是通过求偏导来改变所有的weight致使最后的loss改变,使loss最小。
通过上面的例子我们应该都有一个反向传播的大概轮廓了,接下来回到神经网络的node中。下面这个就是神经网络中任意一个node:
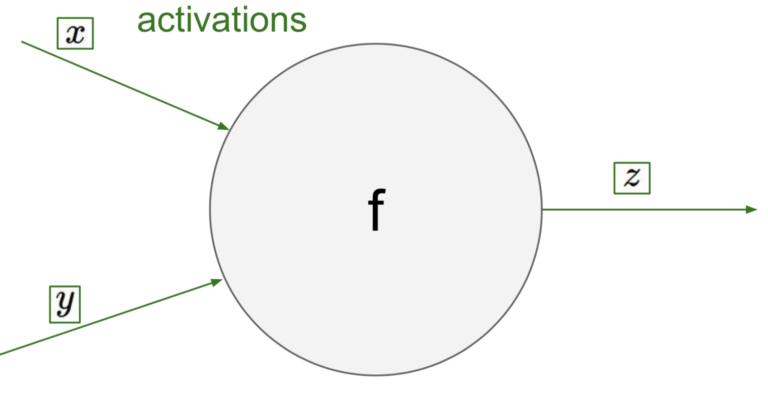
假设有两个输入,一个输出z,f就是一个激活函数比如说sigmoid。我们对这个node做一次反向传播就是:
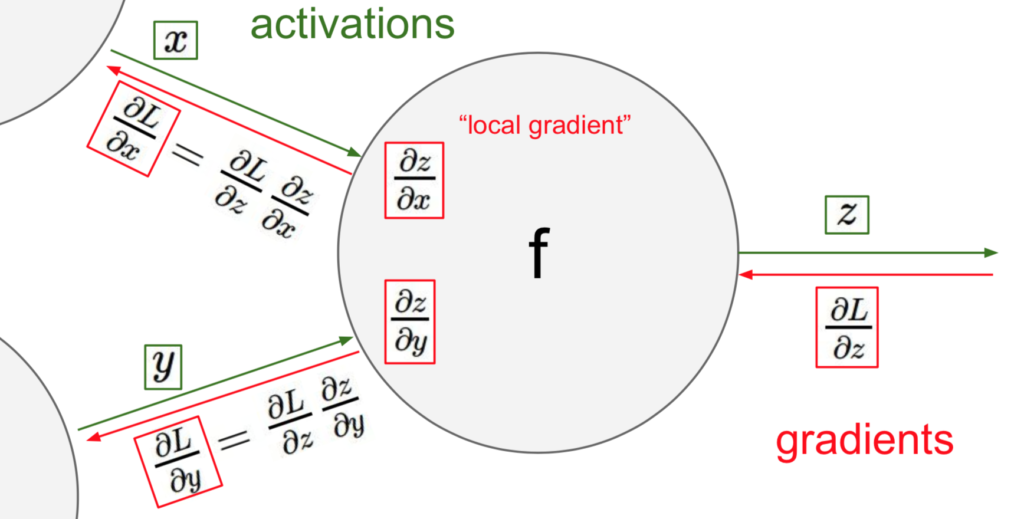
得到loss之后,我们求出来loss对z的偏导,再求出来loss对于x,y的偏导,用chain rule就好。其实就是用local gradient * 输入。
我们现在扩大几个node,比如说我们有这样的公式:
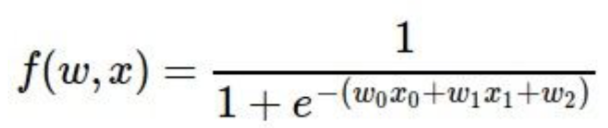
用计算图来表示是这样的:
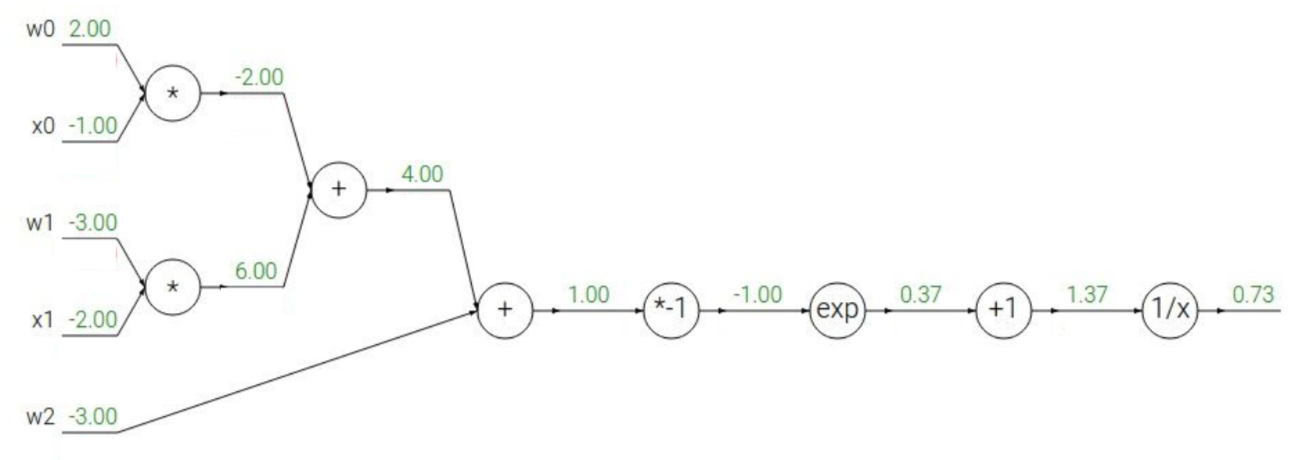
我们像之前一样做一遍反向传播,值得注意的是,这是一个sigmoid函数,我们是不是可以直接求出来sigmoid的偏导不再把它展开写?
当然可以,sigmoid的导数就是 sigmoid * (1 – sigmoid),推导过程也很简单:
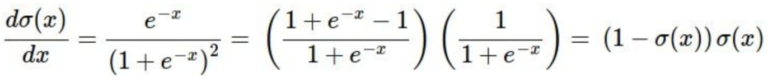
所以整个结果就是这样了:
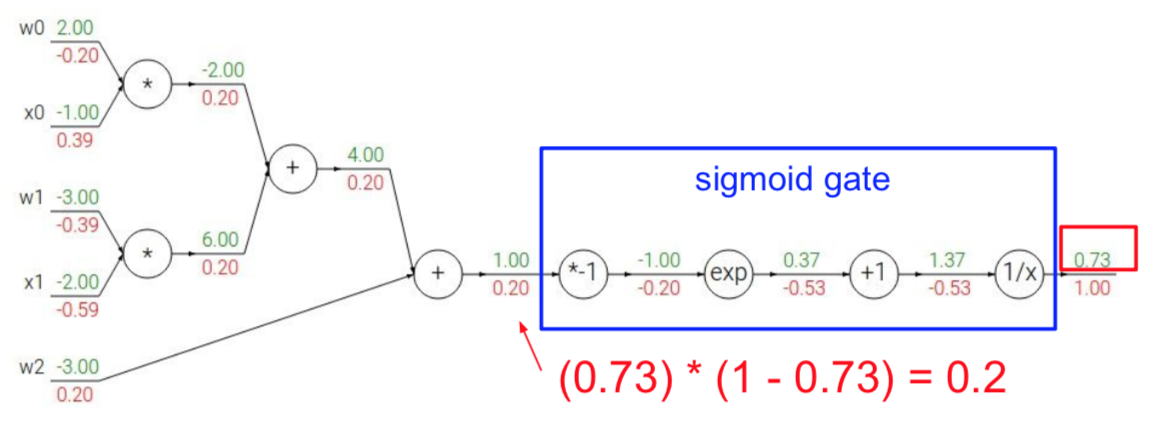
如果以上都可以理解并且掌握了,那么你就对反向传播已经理解了。
- 激活函数
我们前面经常提到这个激活函数,也说过用它来去线性化。所以激活函数的作用就是在线性模型表达力不够强大的时候,去线性化来增强表达能力。
之前提到的激活函数叫sigmoid,这也是逻辑回归中的映射函数。但激活函数不仅仅是sigmoid,还有很多更优化的函数,下面来分别介绍一下:
- sigmiod函数:
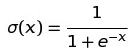
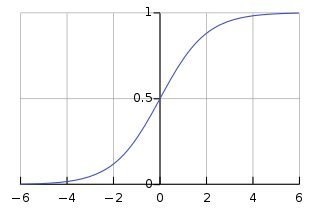
太熟悉了不介绍了。但是虽然用处广泛,它也有很多缺点:1. 易造成梯度消失,比如图中当x = 6/-6的时候梯度为0。 2. 非原点对称,这个性质会导致收敛很慢。3. 因为有exp导致计算代价大。
- tanh函数:tanh(x)
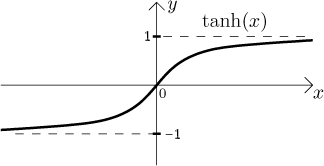
可见tanh函数是原点对称的,所以对比于sigmoid函数,它没有第2个缺点。
- ReLU函数: max(0, x)
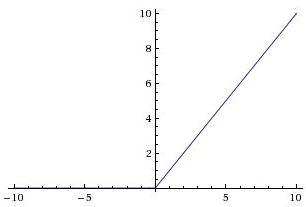
很简单的一个函数,首先能看出来它也是非原点对称的,其次relu的负x轴也会造成梯度消失。但是好处是它的计算速度很快,大约是sigmoid和tanh的6倍。
- Leaky ReLU函数:max(0.1x, x)
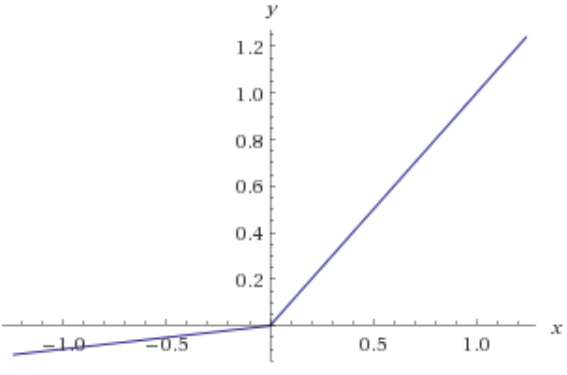
这次左边取的不是0而是0.1x,是不是就解决了梯度为0的问题。这里0.1是个超参数,我们可以根据情况自己选择。
- Maxout函数:
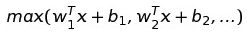
就是所有input中最大的那一个。它具有ReLU函数所有的优点,又避免了ReLU的缺点,可以说是很强大的一个函数。但是强大的代价会很大,它的参数量会double,使整个神经网络更加臃肿。
- ELU函数:
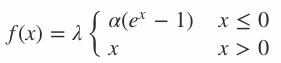
这是个对噪声有很强鲁棒性的函数,但是一样,强大的函数计算量很大。
以上基本是现在工业上经常会用到的激活函数,用得最多的也可以说是默认的是ReLU函数。如果效果不好,可以改尝试Leaky ReLU和Maxout。
经常有人问既然神经网络那么多层,我们可不可以每层用的激活函数不一样?嗯。。讲道理是可以的,但是对于效果来说没有什么变化,也就是说你整个模型的好坏,不取决于你的激活函数用的多么的绚烂,一旦某一个激活函数可以使用,那么再换别的效果也不会有差别。就像跑400米,你每跑100米换不同的鞋,并不会对你的能力产生很大影响。
