宏观理解
朴素贝叶斯模型是一个概率模型,是一个生成模型(Generative Model),背后的数学理论来自于贝叶斯理论。简单来说它计算的就是已知X的情况下,Y的概率是多少,所以一般预测一个值都会计算两个数值概率,分别是已知X的情况下,Y = 1的概率和已知X的情况下,Y = 0的概率。然后我们看哪个概率更高就预测为哪个。
微观分析
学习这个模型第一件事就是贴贝叶斯公式:
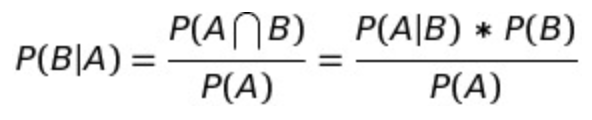
认识一下,在这个公式里有几个组成部分:
| P(B | A):在事件A下事件B发生的条件概率,叫做后验概率(posterior prob) |
| P(A | B):在事件B下事件A发生的条件概率,叫做似然函数(Likelihood function) |
P(A),P(B):独立事件A和独立事件B的边缘概率,叫做先验概率(prior prob)
了解完贝叶斯公式,再看一下贝叶斯准则:
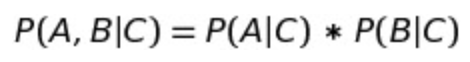
在这里我们要求A, C是相互独立的事件。举个例子,如果我们有一句电影的评价,我么想预测它是积极的还是消极的评价,那么我们就有了下面的计算:
P(“This is a great movie”|negative) = P(“This”|negative) * P(“is”|negative) * P(“a”|negative) * P(“great”|negative) * P(“movie”|negative)
P(“This is a great movie”|positive) = P(“This”|positive) * P(“is”|positive) * P(“a”|positive) * P(“great”|positive) * P(“movie”|positive)
这里面要求每个单词都是相互独立的。
在工程里面,可能概率会越来越小,而且乘法计算消耗时间,那么我们就可以把每个概率取对数:
log(P(“This is a great movie”|negative)) =log(P(“This”|negative)) *log(P(“is”|negative)) *log(P(“a”|negative)) *log(P(“great”|negative)) *log(P(“movie”|negative))
计算出来的概率有可能为0,那么我们可以用拉普拉斯平滑(Laplace Smoothing)。
如果训练的单词太多,可以用stop words,比如上面的 “this”, “is”, “a” 都可能被去掉。
当然如果单词之间有相互依赖关系,我们可以用N-Gram。比如这里用的就是3-Gram:
P(“This is a great movie”|negative) = P(“This is a”|negative) * P(“is a great”|negative) * P(“a great movie”|negative)
最后我们还可以设置出现在不同地方的单词权重不一样,比如出现在标题的权重高一点,文本的低一点。
这些都可以用于对文本分析模型的优化。
