宏观理解
k-近邻算法其实特别容易理解,一个图就能看懂:
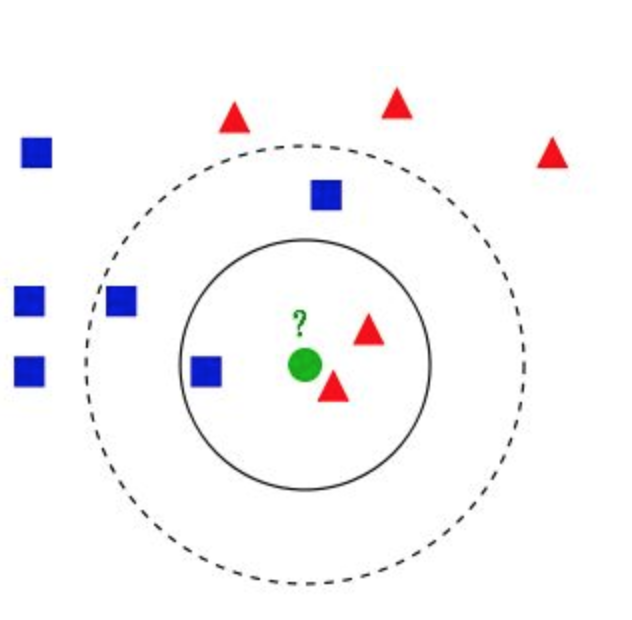
图中我们有两个类别,一个是蓝色的一个是红色的,现在我们要预测绿色的数据点属于哪个类别。很多人看了一眼就会说,红色啊它跟旁边红色靠的那么近。恭喜你你已经理解了1-近邻算法了。什么叫1-近邻,就是按离他最近的那个点,是哪个label的就预测为相同的值。那么如果我让你找3-近邻呢?也就是图中实线以内的数据点。这时候有3个点,一个蓝色两个红色,那绿色应该归为哪类?当然是红色,人多力量大,一个蓝色干不过红色。那么如果我们扩大到虚线以内的点呢?三个蓝色两个红色,这时候红色又吃亏了,所以绿色会被蓝色抢过去。这就是k-近邻算法。其中k是我们一个超参数,它至关重要,决定着绿色点的命运。
微观分析
我们大概知道k-近邻算法在做什么了,现在想一个问题:如果我们没有一个图供可视化,我们怎么找离绿色点最近的k个数据点呢?我们有3种方法:
1.欧几里得距离(Euclidean distance)
就是空间内两个点的绝对距离
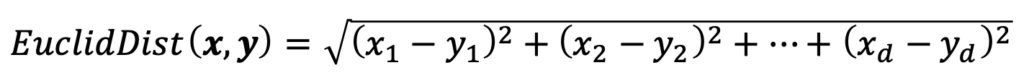
- 曼哈顿距离(Manhattan Distance)
纽约市的道路是横平竖直的,一个个街区都是小长方形,所以名字由此而来
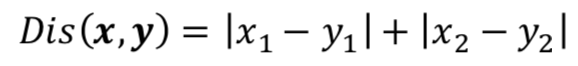
- 余弦相似性(Cosine similarity)
计算两个向量夹角,广泛应用于计算文本的相似性
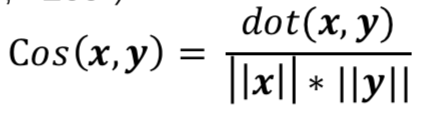
我们知道了所有点对于绿色点的距离就可以找出前k大的点了,进而就可以看谁的数量多就归于哪个类别。
所以整个k-近邻的算法过程就是:
- 初始化数据处理 – 储存所有数据点的内容
- 用一个for loop来寻找最佳的k值,一般不超过20
- 计算距离
- 进行预测
- 检查是否与真实值一样并统计正确率
- 评估正确率
- 找出是哪个k值有最好的正确率
- 进行预测 相当简单对吗?
所以k-近邻的有点就是特别简单易于实现,而且不需要事先训练模型。
当然它的缺点也正是因为它是懒惰算法,而且需要大量内存空间去存储所有的数据点。也因为这个,算法整个复杂度很高,毕竟每预测一个点就要需要所有的数据点。
