宏观理解
我们已经讨论过逻辑回归了,它是个二分类器,在画逻辑回归的决策边界的时候,通常不只有一条线可以分割两个分类。就像这样:
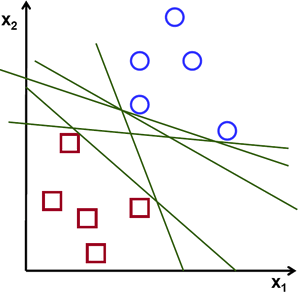
通过这个图我们也能明显看出来,如果让我们自己手画这条边界,我们不会画的这么怪异,比如及其贴近某一阵营远离另一阵营。可是这正是逻辑回归可能给我们的结果,显然科学家们对这个结果并不买账。试想一下如果让你来亲手画一条决策边界,大概应该是这样的才比较舒服:
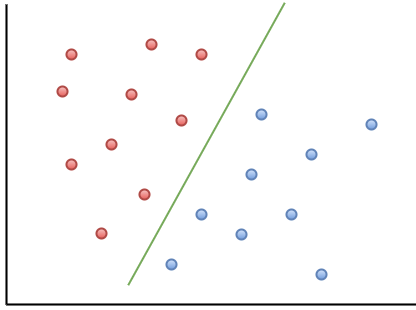
这条线大概处于两个阵营的中间,不偏不倚,对于强迫症来说这就是最美丽的东西。那么支持向量机(也叫大间距分类器)正是强迫症们的福音。它可以帮助我们画出这样一条线,所以用术语来形容svm的motivation叫:maximize the minimum margin。有了这条线,是不是就增强了鲁棒性,对于更多的数据拟合的更好了?
微观分析
这篇文章是按照业界大牛Andrew Ng在coursera上的思路讲解的。因为看了很多网上的文章,感觉数学理论过多不利于初学者理解,所以这里写的稍微入门了些。
现在我们来好好认识一下svm的决策边界:
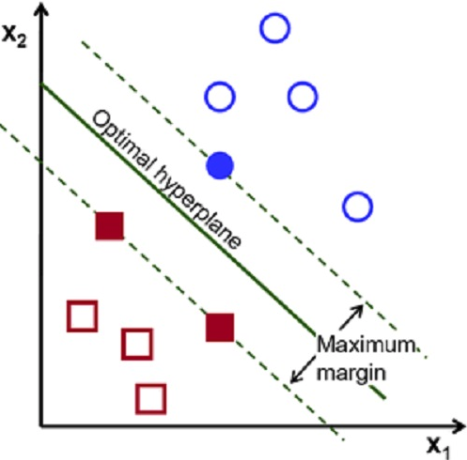
其中绿色的实线就是我们梦寐以求的决策边界,它到两个阵营的距离称之为margin,所以这条线也就是最大化来这个margin。 其中蓝色实心的圆圈和红色实心的正方形叫做支持向量(support vector)。那么怎么来找这条线呢? 很简单,既然这条线是从逻辑回归众多的怪异分界里面选出来的,那么把逻辑回归的损失函数稍加修改就变成来svm的损失函数。 我们已知逻辑回归的损失函数是这样的:
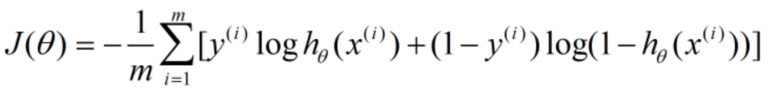
我们把loghθ(x)替换成svm的hypothesis就变成了:
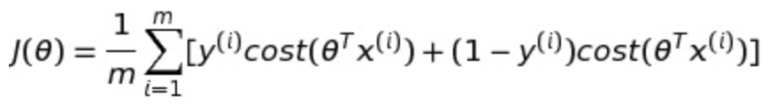
(题外话:这个cost function肯定有很多人会问什么是cost()?Andrew这样讲只是让我们更容易理解,其实svm常用的损失函数是hinge loss或者square hinge loss。想深究的同学可以另外google这个loss这里不做扩展。)
在可视化上,LR和SVM的损失函数可以表现为这样:
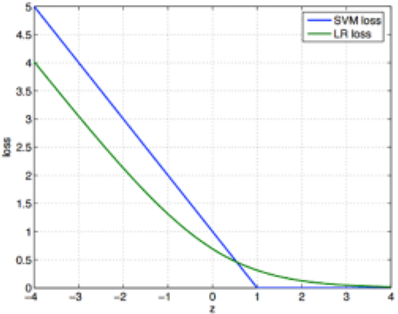
我们已知对于LR来说,
如果预测y = 1的话,那么我们要尽量让hθ(x) ≈ 1,也就是
如果预测y = 0的话,那么我们要尽量让hθ(x) ≈ 0,也就是
由上图可见,我们在SVM中,
如果预测y = 1的话,那么我们要尽量让hθ(x) ≈ 1,也就是
如果预测y = 0的话,那么我们要尽量让hθ(x) ≈ 0,也就是
所以我们可以写出SVM的hypothesis为:
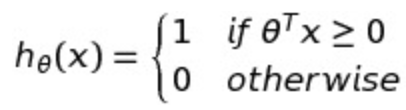
总结一下,现在我们了解了SVM的损失函数和hypothesis对应预测值的关系,汇总一下有了这张图:

最上面是cost function,这个跟我们之前给出的多了一个正则项,按惯例,我们把正则项前面的λ超参数放到了前面的C。这样C = 1/λ。如果C变大,那么说明正则越少。关于正则项的介绍有专门一篇文章这里不做赘述。下面是两个cost function的可视化,左边对应的y = 1,右边对应的y = 0。所以我们有了最下面的两条结论,如果要预测为1,我们要左边的图的横轴z大于等于1;相反对于要预测为0是一样的。
值得注意的是我们想让大于等于1或者小于等于-1,不再是之前逻辑回归里的
大于等于0或者小于0了,我们管这个特殊的1/-1叫做安全因子(safety factor)。
现在我们了解了一个新的机器学习模型的hypothesis、cost function以及决策边界的划分。现在来探讨一下背后的数学原理。
假设我们有两个向量u和v:
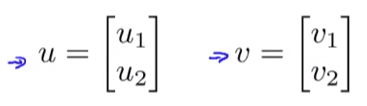
那么他们的向量内积就是,那么它等于什么呢?
我们把u和v可视化出来:
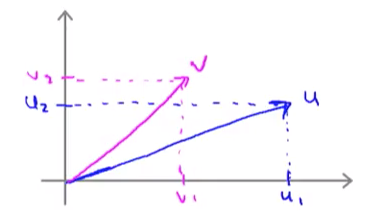
| 我们管 | u | 叫做u的范数,它的意义就是向量u的欧几里得长度,根据勾股定理我们可以计算出来 |
下面我们把v直角投影到u上,当然也可以把u直角投影到v上,这个不影响结果。如下图。
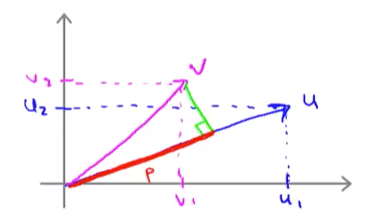
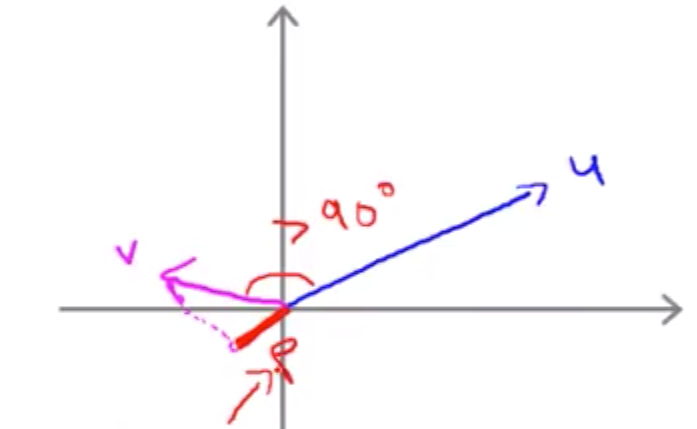
其中红色的线叫做v投影在u上的长度,我们把它的长度叫做p。p是一个有符号的实数,也就是在下图中p是正数,但是p也可以是负数。我们注意到上图中由于v和u的夹角小于90度,所以投影可以直接落在u上,如果这个夹角大于90度,这时候投影就只能落在u的延长线上,此时的p为负。
然后我们可以写作
那么我现在可以把
同理替换成
,我们可以画出下面这张图:
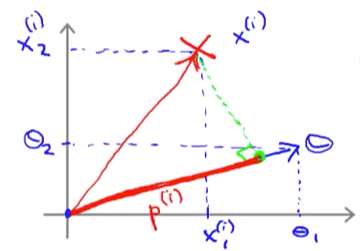
| 因为我们已知在支持向量机中当y = 1的时候 |
θ | ≥ 1 |
那么为什么svm找的最大margin和这个有关系呢?我们假设有下图这样的数据集,然后绿色的线是我们的决策边界, 那么红色和粉色的线段分别是两个label的support vector到θ的投影长度。如果我们要p * ||θ|| ≥ 1,是不是p越小的话,||θ||就要越大?
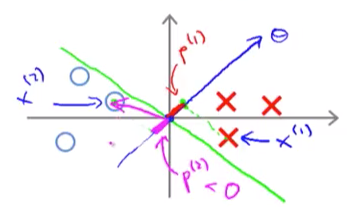
| 可是我们的svm就是要找到一个可以让p尽量大的情况。所以与上图相反,我们要缩小 | θ | 。比如我们把决策边界换成y轴: |
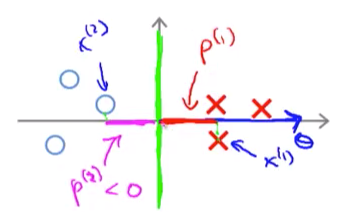
| 这样是不是就是我们希望的决策边界?此刻的p比之前的p要大了许多,所以相应的 | θ | 也就变小。SVM就是要找到这样的 | θ | 使得我们所有的p最大。 |
SVM with kernel 介绍完来基础的SVM,有人可能会问,以上画的决策边界都是直线,那就是只能用在线性可分数据集上,那如果我的数据集线性不可分怎么办? 没关系我们SVM还有一个绝招叫核函数(kernel function)。核函数在做的,就是把低纬度线性不可分的数据集映射到高纬度线性可分。举个例子:
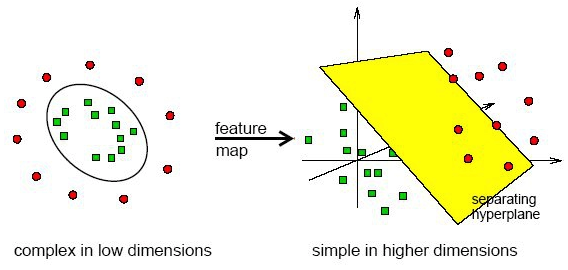
先来句鸡汤,当你遇到困难束手无策的时候,不妨换个角度看问题,你会发现世界原来还可以这么简单。
这就是核函数告诉我们的真理啊。你想如果是二维的,我们怎么可能用一条线分开?明明这是个圆啊。可是如果我们换个角度,用三维来看待问题,是不是很容易就可以找到一个超平面来分开两个阵营。
回到问题上,假设我们现在有的是一个线性不可分的数据集,比如是这样的:
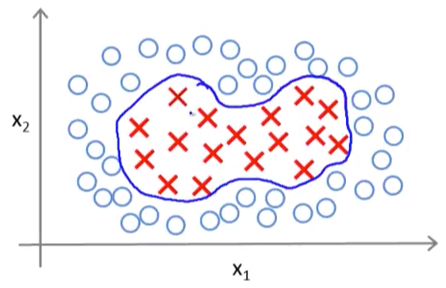
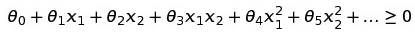
我们来做一个替换:f1 = x1,f2 = x2,f3 = x1x2,f4 = x1^2,f5 = x2^2。所以我们有:
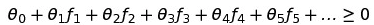
这里我用高斯函数来举例。我们已知所有的feature x,那既然要映射到高维空间,就必须对已经有的数据点进行一个转换。假设我们有这样3个新的数据点l1,l2,l3:

f2和f3同理。这里的similarity就是我们的核函数,这里用的是高斯核函数。
如果x和l的相似度很高,那么在高斯函数中分子的norm就约等于0,那么整个f就约等于1;如果x和l的相似度很低,那么在高斯函数中分子的norm就很大很大,那么整个f就约等于0。
所以通过了similarity函数,我们可以得到所有的f值,然后我们把这些f值当成新的x参数。假设我们现在有一个l1如图,在3d图中,如果x和l的相似时比如都是[3, 5]。那么f1就是1。如果x离开[3, 5]这个点,离得越远,曲线越平滑,也就是对应的f1值越趋近于0。
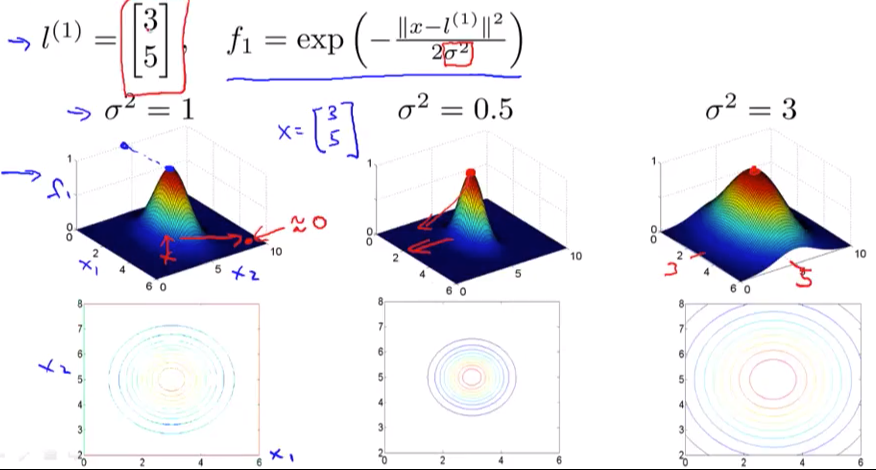
高斯函数里面的σ是一个超参数,但是要说明的是它的变化会导致什么。比如上图中我们改变σ从0.5 ~3。可以明显看出来如果我们的σ很大,那么f曲线会很平缓,bias会很高,variance会很低;相反σ很小,那么f曲线会很陡峭,bias会很低,variance会很高。
那么这个f怎么帮助我们来分类呢?假设我们有下图中的三个l1,l2,l3,还有一个已知的预测函数和学习到的每个θ的值:
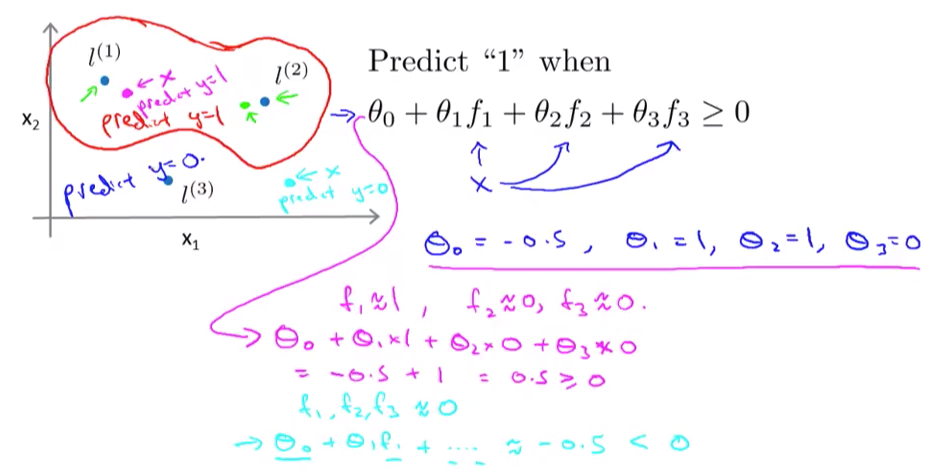
那么现在我们假设有一个粉红色的点x,它离l1最近,所以我们根据前面的图可知道此时f1趋近于1,相反,它离l2和l3很远,可知f2,f3趋近于0。套入公式也就是粉色字体,得数是0.5。因为大于0,我们预测x为1。类似的,对于淡蓝色的点,离3个l都很远,那就都是0,最后只剩下一个截距-0.5,那么小于0我们就预测为0。
如果你尝试多一些数据点你会发现,越靠近l1和l2的点会趋近于1,那么我就知道这个决策边界就像红色曲线画出来的近似了。
对于怎么选择l1,l2,l3,我们可以直接把他们和x1,x2,x3划等号,然后在cost function中对应的每一个x,此时就变成了f:
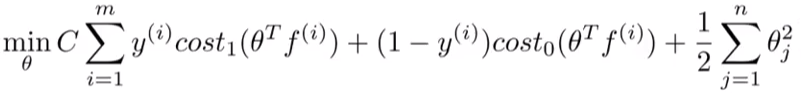
这个f当然和x不一样因为f = kernel(l1, x1),这要看我们选取什么样的核函数了。
以上就是在svm中加入kernel function的原理。
SVM中的拉格朗日对偶
可是怎么求解这个超平面的参数呢?我们就可以把原始优化问题找到另一个更简便也可以替代原始优化问题的对偶函数来解决。
我们把样本点到分界线的距离写为d,通过几何间隔求出
所以能看出来,如果我们要最大化间距d,那么就等于最小化w,所以我们有了我们的目标函数(为了求导方便,我们改写函数):
又因为在超平面上无论我们怎么映射x,都会存在两个不等式:
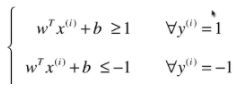
所以通过这个我们可以得出
我们就有了有约束条件的优化问题,并且代入到拉格朗日函数中,得到原始问题和对偶问题。 如果对偶不熟悉的话可以参考凸优化和对偶这篇文章,写的很详细。
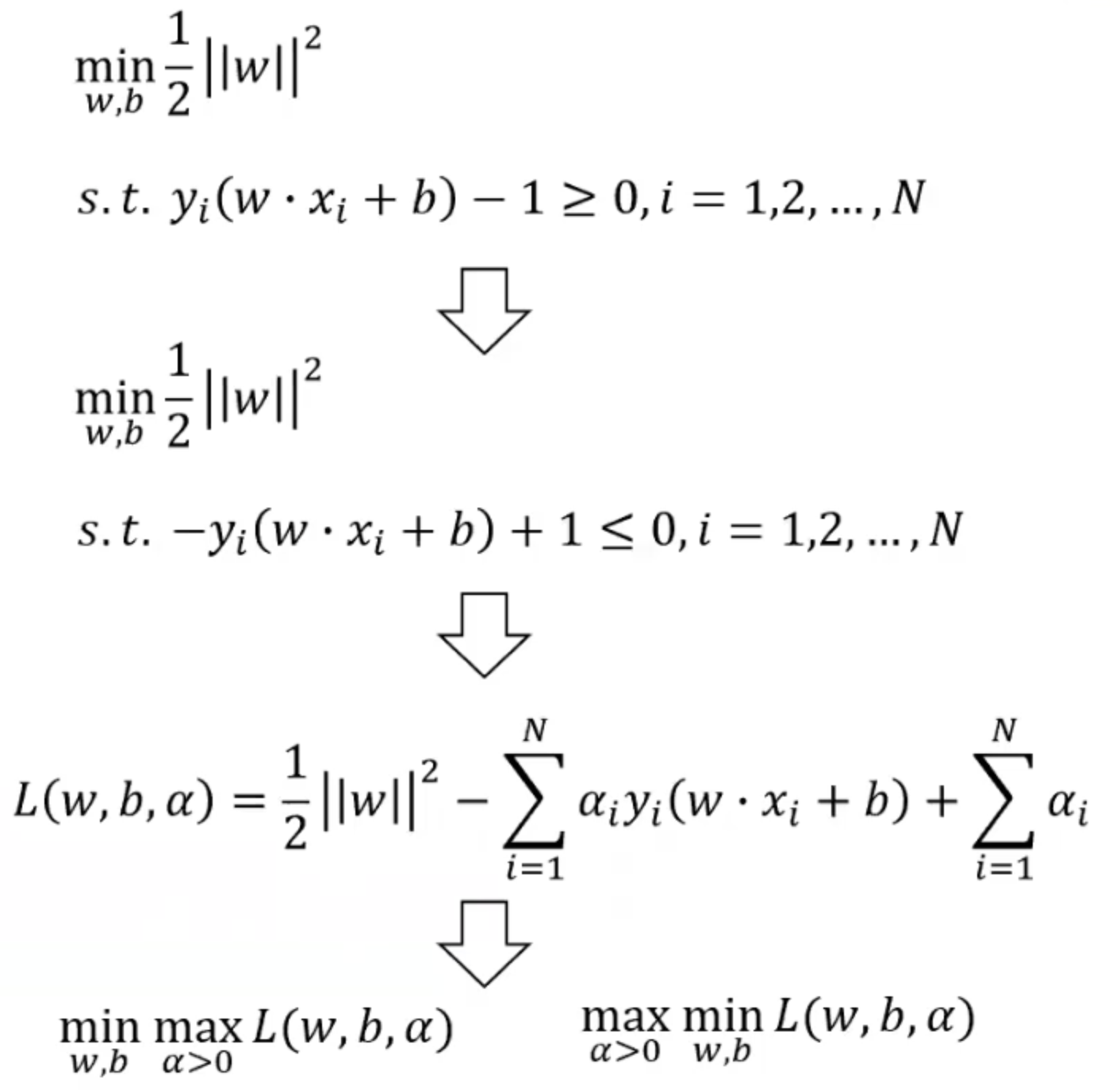
随后我们试着求解min L(w,b,alpha),计算出拉格朗日函数关于w和b的偏导数:
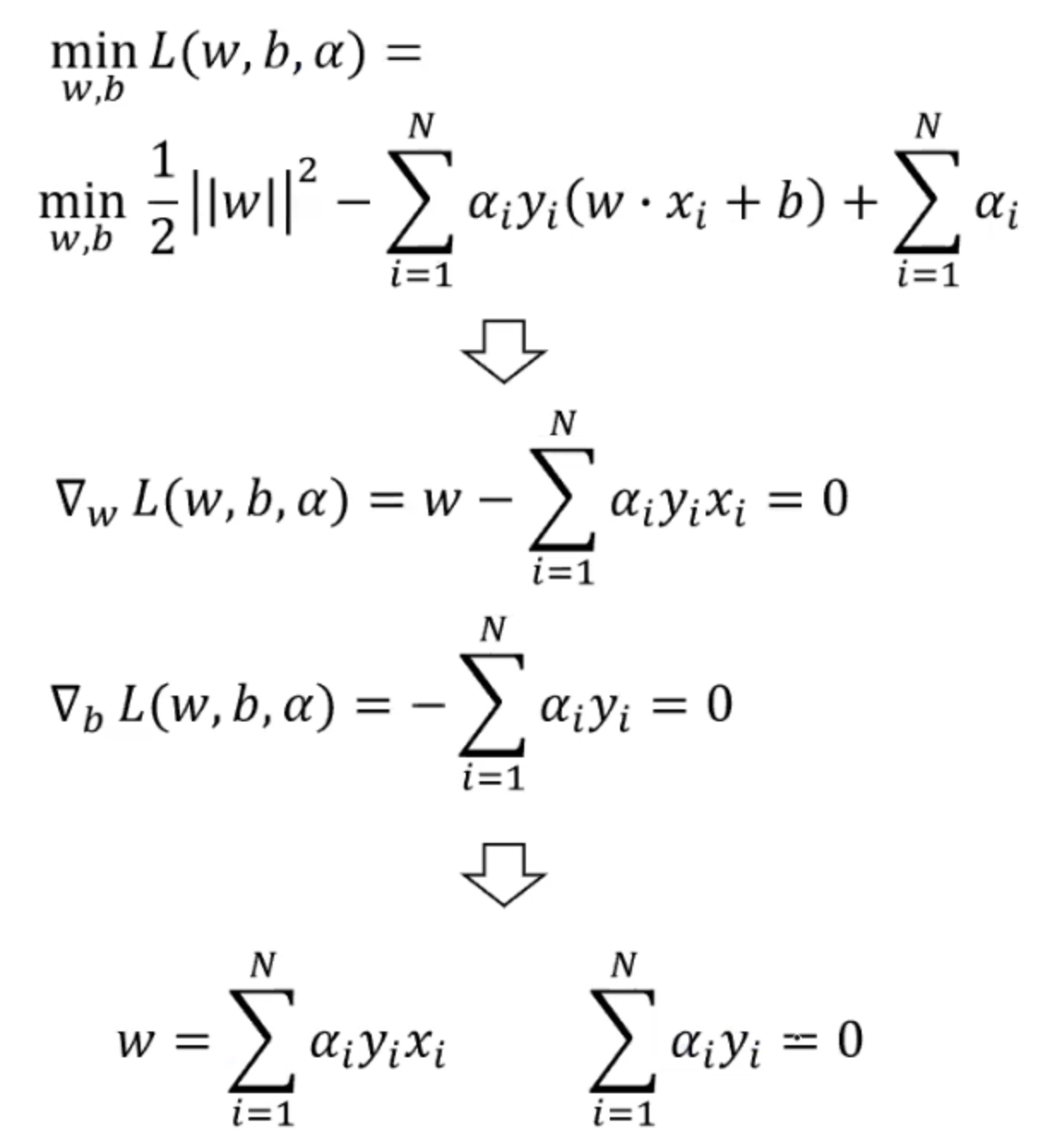
随后我们把得出的w值代入到拉格朗日函数中:
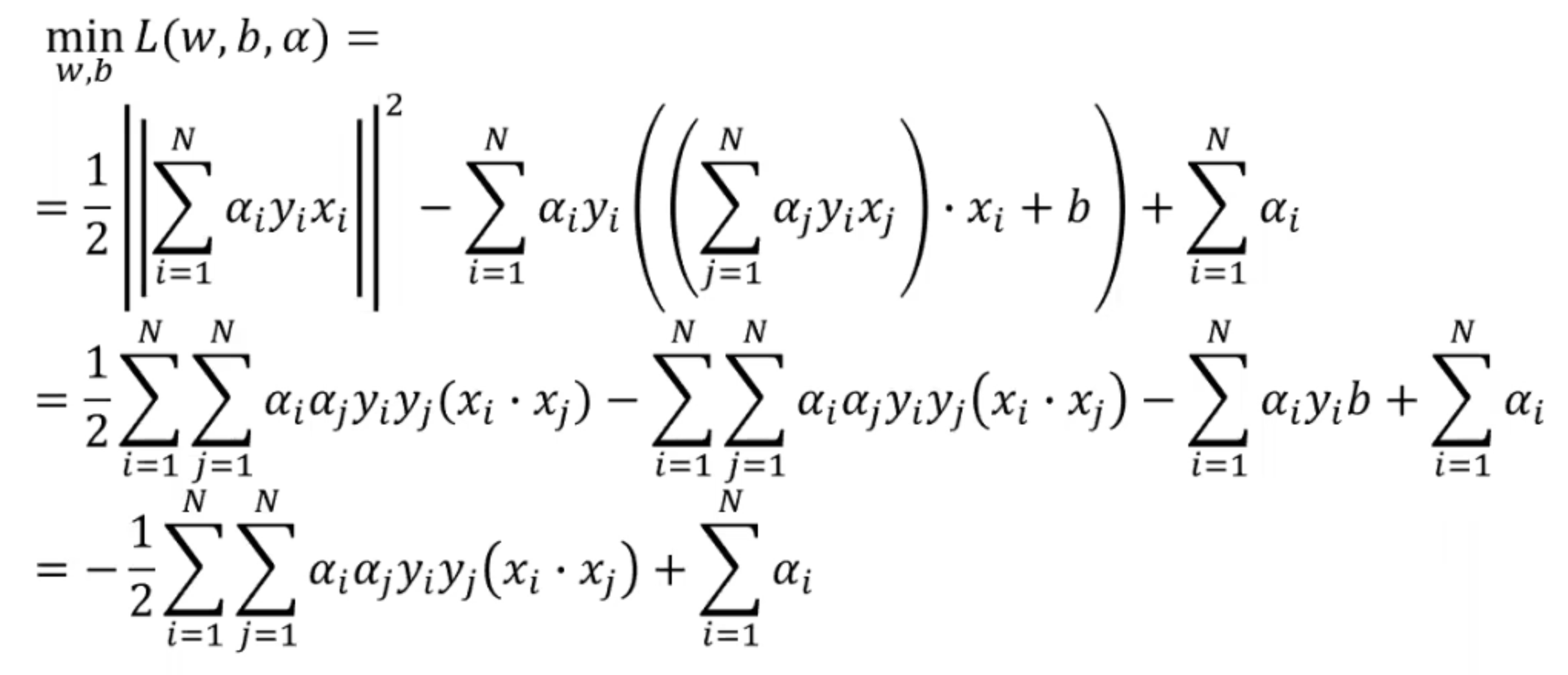
随后我们的原最优化问题的对偶问题就变成了:

因为我们知道它是满足slater条件的,所以我们可以通过KKT条件进一步解出
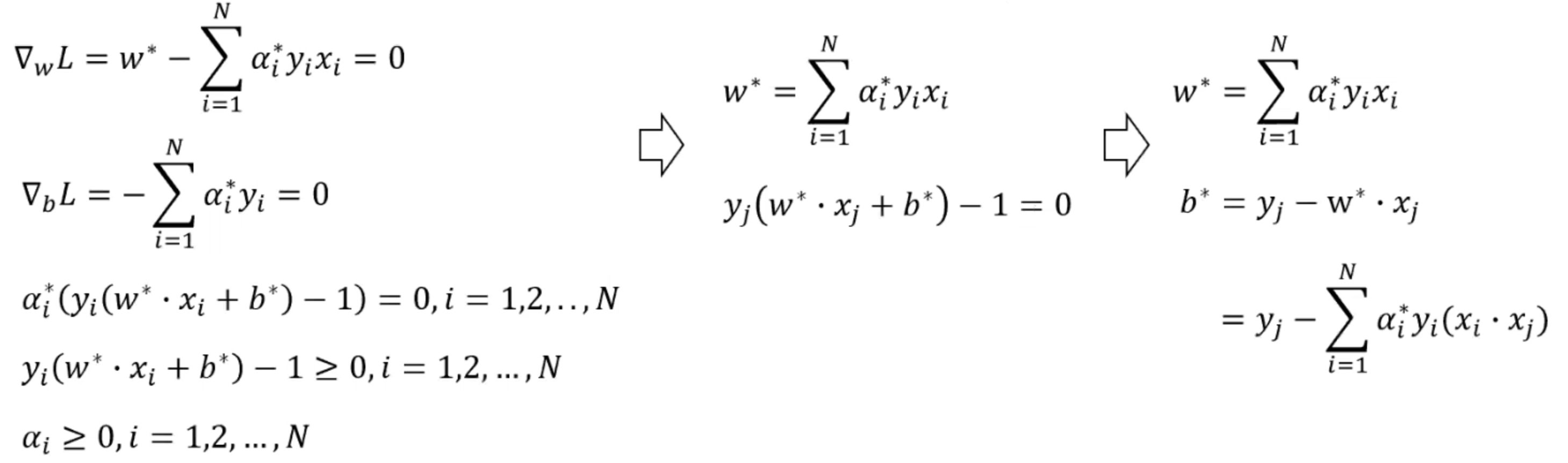
所以通过求得对偶问题,我们最终可以把一开始的分离超平面改写成:
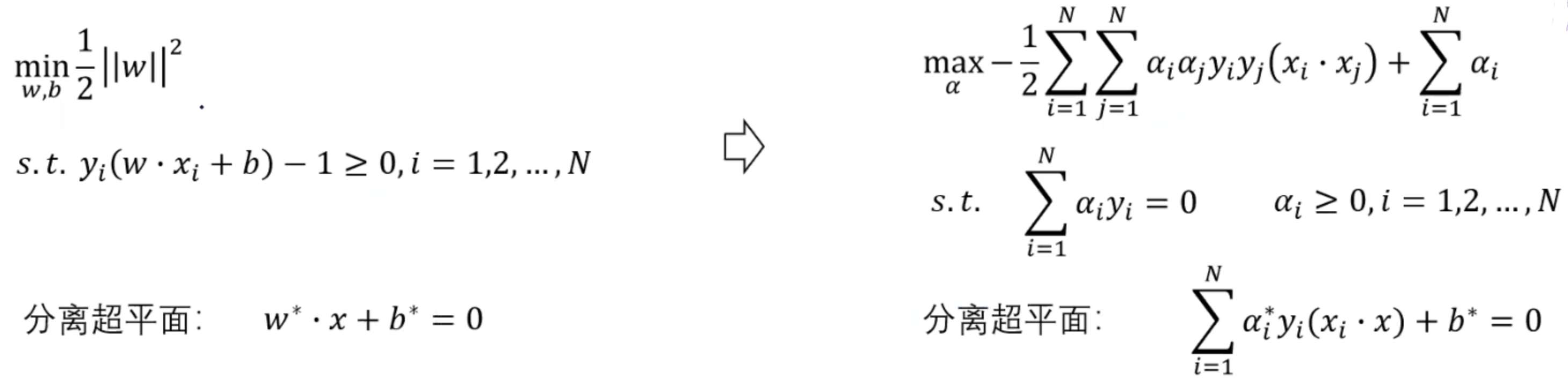
此时我们的x都是二维平面的数据点,经过三维的某种映射我们可以写成,我们进一步发现
在分离超平面中,有关的数据点x是由内积组成的,故我们可以简化这个x数据点映射用
代替。
所以问题变得简单了,我们输入空间到特征空间的变换,其实就是在选择这个K函数是什么样的核函数,比如常见的核函数有高斯核函数、多项式核函数等。
