宏观理解

逻辑回归是一个分类模型，也是一个广义上的线性模型，用于处理线性可分的数据，输入特征往往都是多维互相独立的。它在线性回归的基础上，把结果映射到了0～1之间，所以多用于二分类任务，毕竟多分类的时候有softmax。这种映射关系其实上是概率的映射，大于0.5的概率，就预测为1，小于0.5的概率，就预测为0。之前提过线性回归的训练过程是最小化所有θ到决策边界的平均距离，而逻辑回归模型的过程则是尽可能的让真实值为1的实例的预测概率无限趋近于1，让真实值为0的实例的预测概率无限趋近于0。

微观分析

逻辑回归的hypothesis就是：。其中这个g()函数就是可以把任何值映射到0～1之间的sigmoid函数。sigmoid函数的图如下：

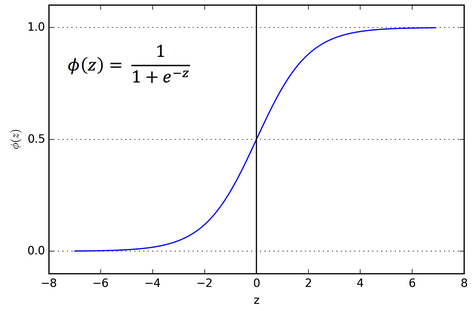
我们把我们的线性回归hypothesis代入这里就是：

有了线性回归的理论基础，我们可以直接给出逻辑回归的损失函数，即交叉熵函数（cross entropy）：

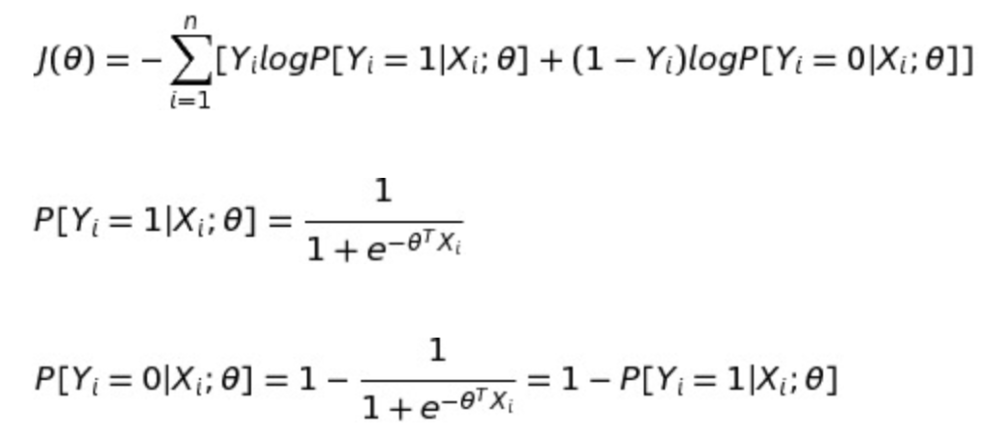
逻辑回归的优化方法一样我们使用梯度下降法，区别就是它的cost function和在梯度下降专题里示例的MSE不同，但本质一样，求个导就好，所以在下面的介绍中，就把重点放在里交叉熵函数的梯度下降推导：

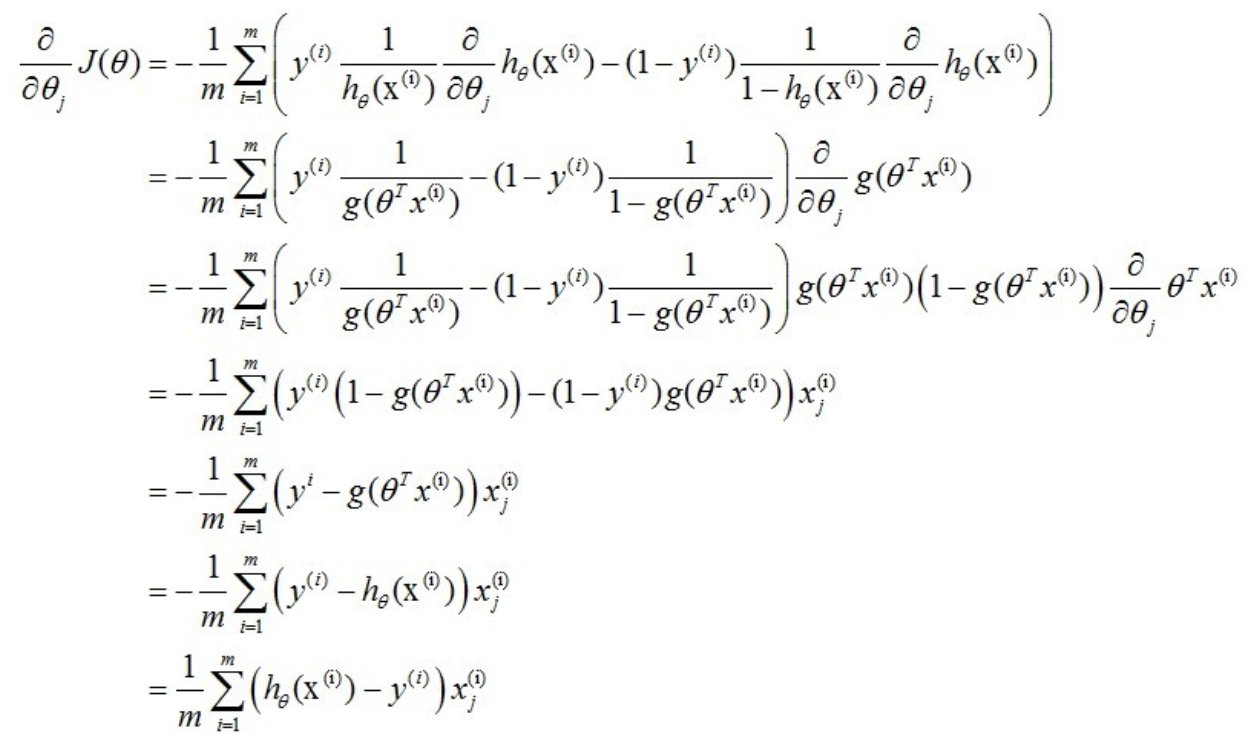
在梯度下降章节我们说过每次迭代的就是：

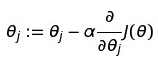
所以在这里我们把损失函数的求导代入最终就变成了：

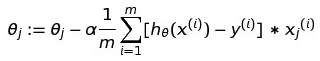
加入正则后

加入正则项后的逻辑回归有两个最为出名，一个叫Ridge岭回归，一个叫Lasso回归。分别是加入了L2和L1的正则项。

Ridge岭回归: 其中的正则项在梯度下降中可求出偏导，故而可以使用梯度法来进行优化。

Lasso回归: 但是其中的正则项求偏导需分段求导，分为3种情况。故无法使用梯度下降求导。所以通常我们都是用坐标下降法来更新每次迭代的某个w参数。

知识点拓展

逻辑回归属于广义线性模型，很多人搞不清楚什么才能叫线性模型？N元N次函数叫不叫线性？多项式回归算不算线性模型？都算。线性模型并不是拟合出来是线性的决策边界才叫线性，也不是所有的参数都是线性的就叫线性模型，而是每一个θ只会影响属于它自己的那个x。想想我们的线性回归和逻辑回归，每一个θ的改变是不是只会影响它后面的一个x？相反，我们说神经网络是由很多个逻辑回归组成的，那为什么不能算线性模型？因为在它进行forward prop的时候一个x不单单只受一个weight的改变而变化。

再来说一个面试中常考的考点，就是在我们使用LR的时候，为什么需要把连续特征离散化？

1. 因为通过离散化，可以让数据更有意义，比如有一个特征是年龄，25岁一定就不29岁的小么？不一定，那么通过离散化处理都会属于同一个区间比如[20,29]。
2. 因为可以做更多的特征交叉，比如城市特征和年龄特征，我们可以交叉来创建新的特征比如：北京&年龄[10,19], 上海&年龄[10,19]。。。
3. 因为稳定性会更好，防止了很多微小的噪音，比如本来年龄是21结果给统计成了28，离散化之后就不会有区别了。