宏观理解
决策树是一种分类模型,很直观,如果是A就往左走如果是B就往右走。举个例子,我们应该都玩过一种游戏,过程是你来猜答案我说是或者不是。比如我们要猜一个人的名字,那么过程大概如下:
问:是男的么? 答:是
问:是演员么? 答:不是
问:是歌手么? 答:是
问:有胡子么? 答:是
问:是腾格尔么?答:是
通过这样的问答我们可以逐渐的把答案缩小,离正确答案越来越近。决策树的本质和这个一样,通过对一些特征的判断,每次舍弃一些可能性。 我们也可以把这个例子构建成一棵树:
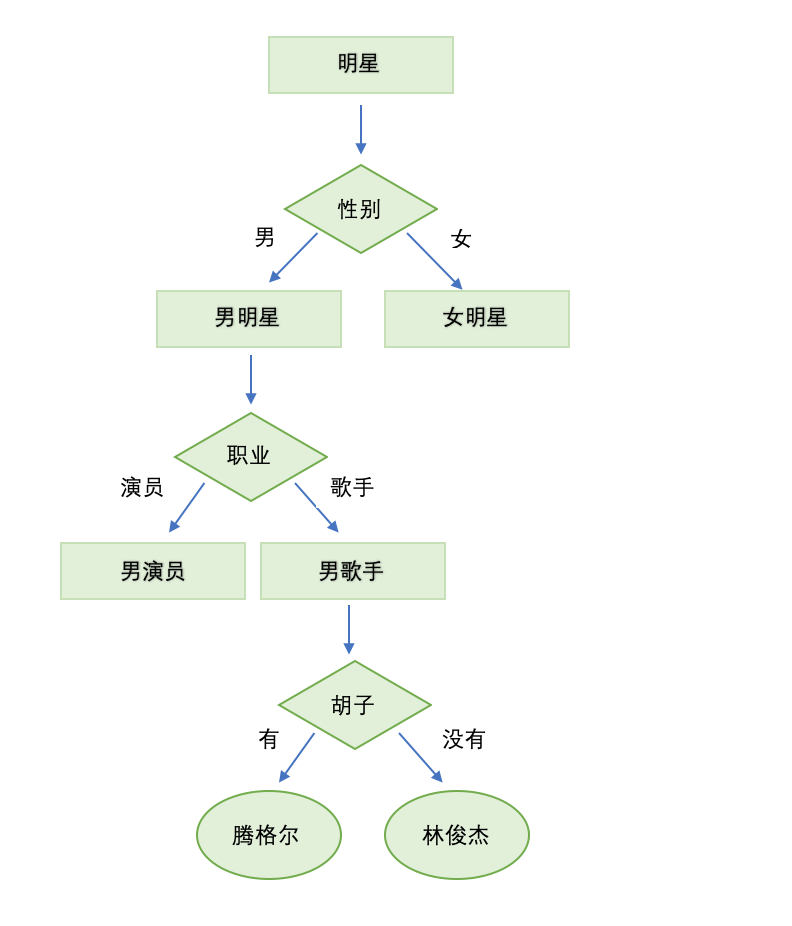
这个树里的所有问题,对应数据集里的features,比如性别,职业,最后圆圈里面的答案就是我们的预测。决策树的这个树的构建过程,就是这个模型的学习过程,其实决策树不是一个应用很广泛的模型,因为决策树你永远可以在训练集上准确率达到1.0,这样非常容易过拟合,造成测试集准确率很低。
微观分析
我们现在来从0构建一颗决策树,已知我们有如下的数据集:
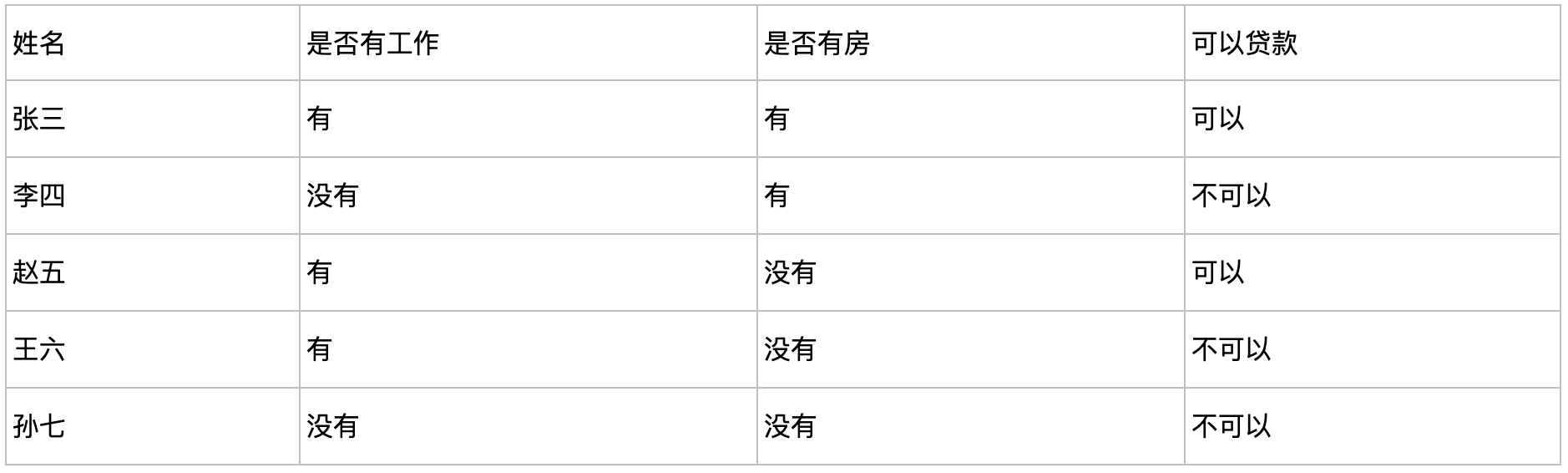
遇到的第一个问题就是,拿哪个feature来做树根(root)呢?有两种方法,第一种是根据正确率:
- 根据工作
有工作:{张三(可以),赵五(可以),王六(不可以)} -> 可以给贷款
没有工作:{李四(不可以),孙七(不可以)}-> 不可以给贷款
正确率个数 = 4
- 根据房产
有房产:{张三(可以),李四(不可以)} -> 可以给贷款
没有房产:{赵五(可以),王六(不可以),孙七(不可以)}-> 不可以给贷款
正确个数 = 3
所以如果按照正确率的方法,我们应该把工作当成树根。第二种方法就是应用最多的,根据信息增益(Information Gain)来选取。那么我们要先了解几个概念:
- 信息量(information)
- 可以想象,如果一件事情发生的概率越低,那么信息量就越大。反之,如果我非常确定明天太阳还会升起,那这个信息量就等于0,和废话一样。
- 熵(entropy)
- 熵其实就是信息量的期望值。
- 信息增益(Information Gain)
- 也就是我们如果按工作来划分的话,我们要计算划分之前的熵减去划分之后的熵 现在我们可以基于以上的公式来用第二种方法划分:
划分前的熵 E = P(可以) * I(可以) + P(不可以) * I(不可以) = 2/5 * -log(2/5) + 3/5 * -log(3/5) = 0.292
- 根据工作
有工作:{张三(可以),赵五(可以),王六(不可以)}
没有工作:{李四(不可以),孙七(不可以)}
E(有工作) = P(可以)I(可以) + P(不可以)I(不可以) = (2/3) * -log(2/3) + (1/3) * -log(1/3) = 0.276
E(没有工作) =P(可以)I(可以) + P(不可以)I(不可以) = (0) * -log(0) + (1) * -log(1) = 0
E(按工作划分后) = (3/5) * E(有工作) + (2/5) * E(没有工作) = (3/5) * 0.276 + (2/5) * 0 = 0.167
- 根据房产
有房产:{张三(可以),李四(不可以)}
没有房产:{赵五(可以),王六(不可以),孙七(不可以)}
E(有房产) = P(可以)I(可以) + P(不可以)I(不可以) = (1/2) * -log(1/2) +(1/2) * -log(1/2) = 0.301
E(没有房产) =P(可以)I(可以) + P(不可以)I(不可以) = (1/3) * -log(1/3) +(2/3) * -log(2/3) = 0.276
E(按房产划分后) = (2/5) * E(有房产) + (3/5) * E(没有房产) = (2/5) * 0.301 + (3/5) * 0.276 =0.286
最后我们分别用划分前的减去划分后:
IG(工作) = E(划分前) – E(按工作划分后) = 0.292 -0.167 = 0.125
IG(房产) = E(划分前) – E(按房产划分后) = 0.292 -0.286 = 0.006
IG(工作) > IG(房产)
所以我们还是把工作当成root。
在选取完root之后,我们可以得到两个leaf:
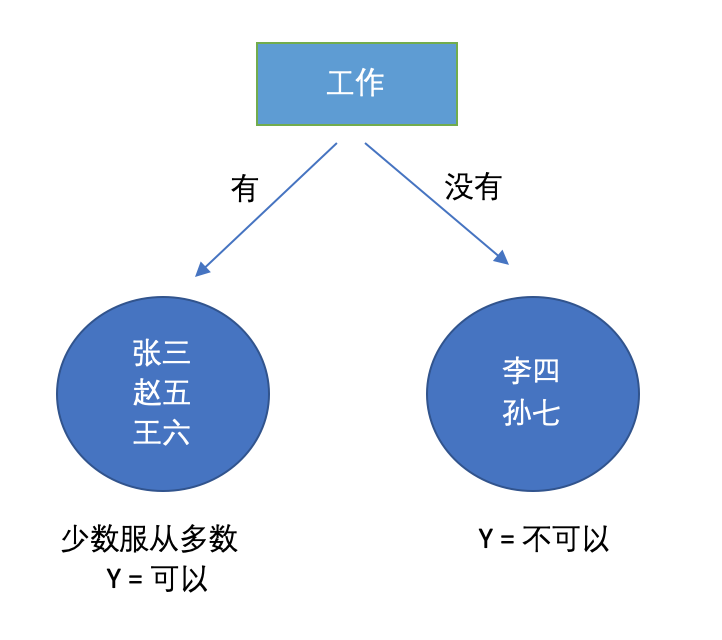
接着我们重复刚才的计算过程,在有工作的分支下继续split,没有工作就不需要了毕竟已经全部正确了。这就涉及到一个问题,我们要split到什么时候?如果继续split不就像之前说的,肯定能得到100%正确率吗,这样不就过拟合了吗?是的,所以我们需要在适当的时候停止决策树的划分,一般来讲我们有几种条件可以终止划分:
最大深度(maximum depth):之前我们按工作划分的树深度为1,这里可以自己设置当深度为多少的时候停止划分,避免过拟合。 最小节点大小(minimum node size):即在一个节点里面有多少个instance,比如上面的图中有工作的node中的size = 3, 没有工作的node中size = 2。当我们reach 到最小的个数的时候就可以停止划分。 错误率大小(error reduction):即在leaf node中的正确率达到了一定的要求,比如有工作的node正确率达到了66.66%,没有工作的node达到了正确率100%,我们可以设定一个阈值比如90%,超过这个正确率就停止划分。 没有更多可用的特征用来划分:顾名思义,都没特征了你拿啥划分。 这几种方法没有哪个更好,机器学习的策略永远都是因地制宜,如果你想避免overfitting前三个肯定是最好的选择。
到目前为止我们遵循以上的循环过程应该已经可以手算构建出一颗决策树了。
补充一些额外的概念和小技巧:
- 一颗决策树的复杂程度由什么来决定呢?叶子节点个数来决定。如果两颗决策树的准确率相差无几,那么当然选择叶子节点少的来用,这个显而易见的道理又叫做奥卡姆剃刀准则(Occam’s Razor)。当然这个不局限于决策树,对于所有的机器学习模型都适用。
- 决策树作为一种没多少数学就能阐述清楚的模型,优点就是简单,所以工业界首选的模型中就有决策树,而且中间过程很好理解。缺点则是在构建树的过程中,一旦用过的特征,比如工作,后面就不能在使用了,所以这也导致了决策树的泛化能力相对较差。
