宏观理解
梯度下降是一种优化算法,在很多的机器学习模型中我们都有损失函数,我们也说过我们希望这个损失函数可以最小化,这样预测值就会离真实值越来越近。 显然我们不能通过一个公式就求得出所有θ的最优值,那么既然一步不能到位的事情,为啥不一步一步慢慢来呢?梯度下降正是完成这个任务的迭代算法。 有人会问,既然每次更新模型参数之后都会有一个新的预测值,那为什么不用每次的错误率来当损失函数呢?慢慢的降低错误率不也是慢慢优化的过程吗? 不是这样的,一个根本的原因在于如果使用错误率,那么整个损失函数就是不可导的,既然是不可导的怎么做梯度下降?也就不能做优化了。 值得注意的是,只有损失函数是凸函数(convex function)的时候才可以用梯度下降找到局部最小值。啥叫凸函数?
凸函数性质:
- 在二维凸函数的最小值的x坐标的左边的x坐标对应的函数斜率是负数,在二维凸函数的最小值的x坐标的的右边的的x坐标的函数斜率是正数
- x坐标越接近于最小值的x坐标,对应的斜率越接近于0
先放个图直观了解一下梯度下降:
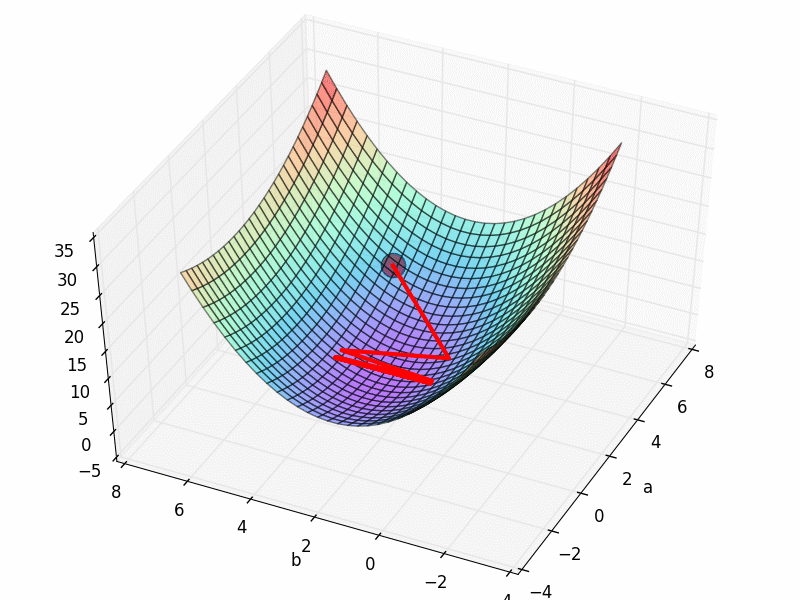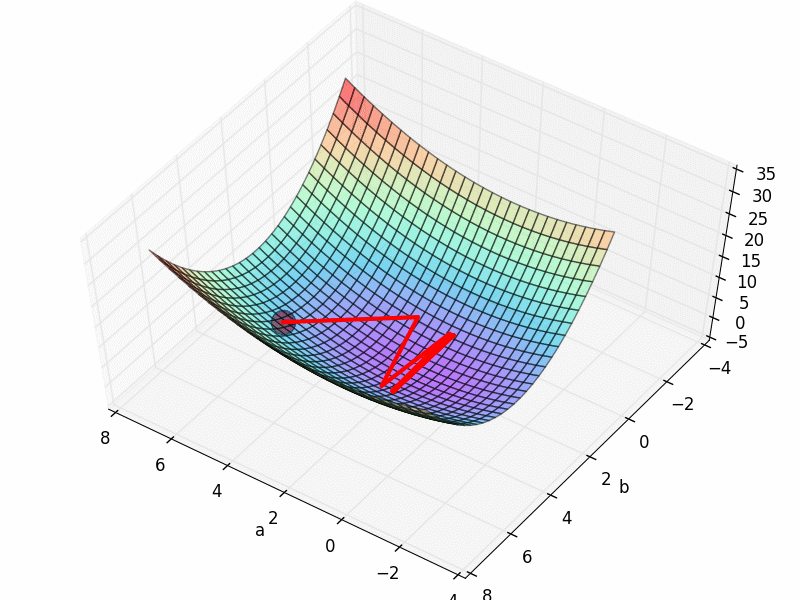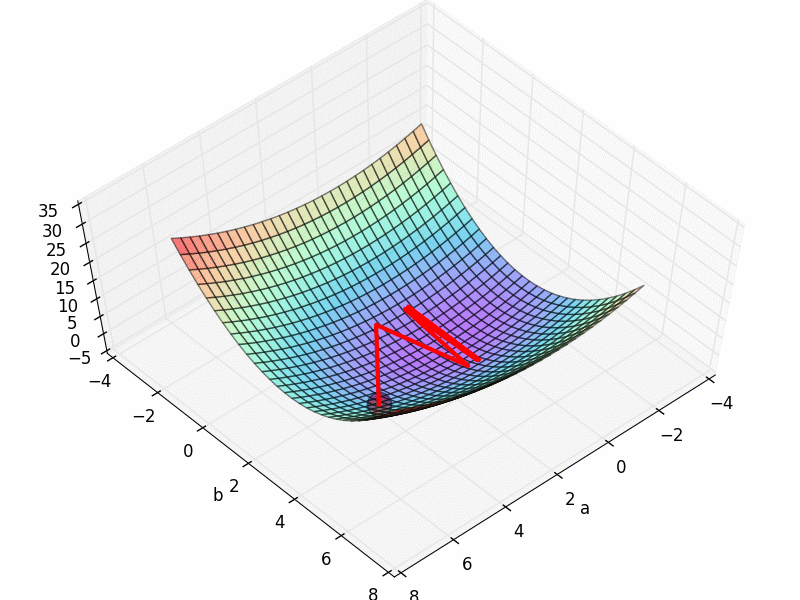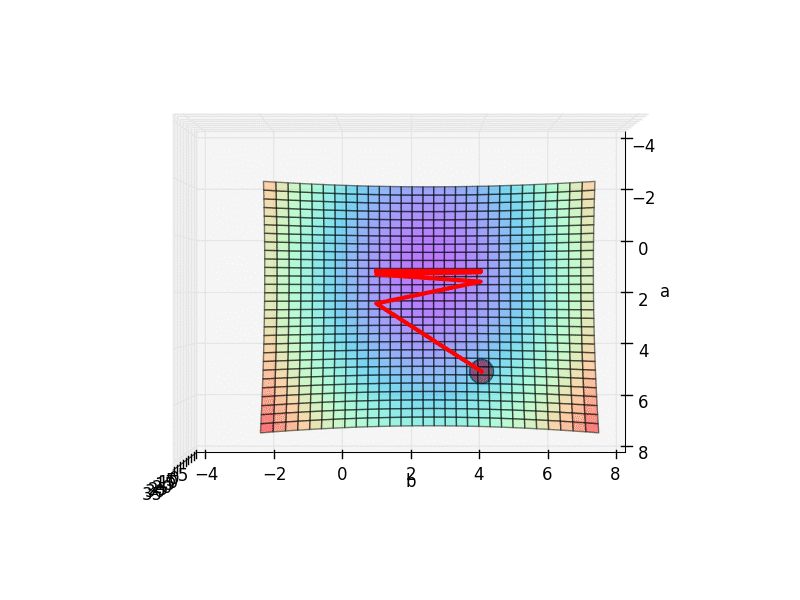
这就是一个属于凸函数损失函数,它呈现出一个碗的形状,正因为这样它才会有最低点,我们才能逐步的去找到这个最低点。 想象这是一块布,四个人拽着四个角,布中间稍微往下沉,这时候我们在任意位置放一个小球上去,这个小球会滚动通过一条路径最终停止在最低点上。 在数学里这条路径可以通过梯度下降找到。有没有想过如果不止一个局部最低点怎么办? 这种情况特别多,尤其是在深度学习中一不小心就会栽进局部最优而不是全局最优,我们抽象出来这张图:
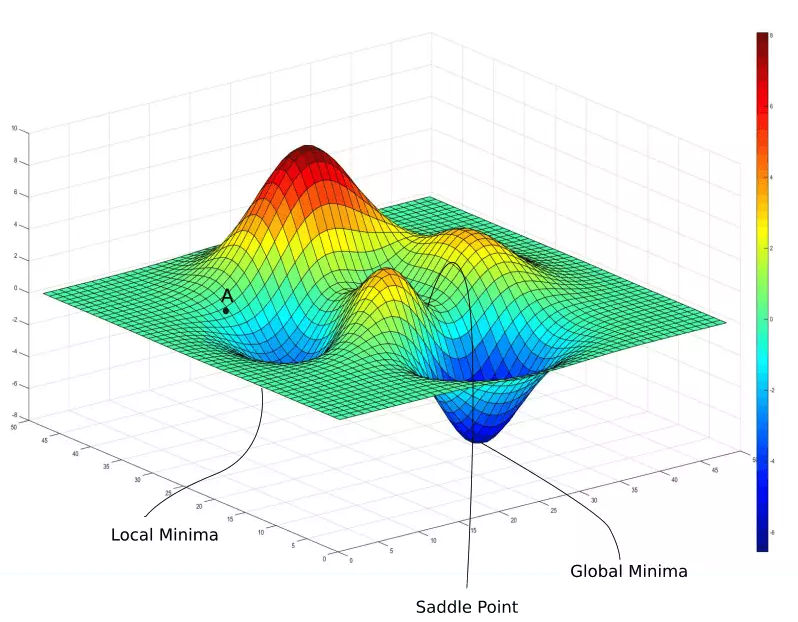
现在我们有的不只是凸函数那么简单了。假设我们从A点出发放一个小铁球,它会滚到哪?当然是面前的局部最优解(local minimum)。你要非说能滚到全局最优那就是抬杠。可是这不是我们想要的,人性是贪婪的,科学家才不会接受这种结果,他们想出来很多方法,比如随机重置一个初始值,看看是不是还是到了同一个点,我们可以重置10次,如果有一次到了全局最优(global minimum),那么我们就知道应该使用这条路径,之前的都不靠谱。这些我们会到之后的深度学习里再做介绍,在这篇文章里我们只关注第一种凸函数的梯度下降。
微观分析
我们使用人尽皆知的损失函数MSE来演示梯度下降的过程:
我们已知一堆特征(feature)x和标签(label)y,然后使用MSE做损失函数,则有如下表达式:
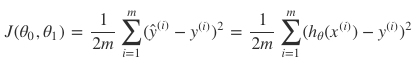
如果想让损失函数越来越小,那么是不是要像这样去更新每一个参数θ:
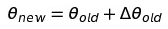
那么这个Δθ是什么呢?就是这个θ对于损失函数J的导数。
我们要做的是对这个损失函数求导,让所有参数的值沿着负梯度的方向(也就是我们之前说的小球滚动的路径)走,直到走到最低点。因为我们要每个参数都下降,所以我们要把每个θ在损失函数上求导,然后让之前的参数θ加上这个负梯度:
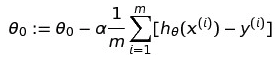
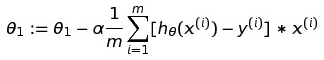
我们重复这个操作直到收敛(converge),就是直到停止到局部最优。推导过程就不放了,无非就是把平方和之前分母的2抵消掉。那么对于多参数的损失函数,用一个公式就可以表达:
Repeat until converge{
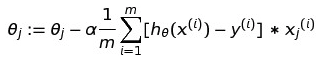
}
必须注意的是,这里的每个θ都必须是同时(simultaneously)更新的,也就是说先不要把θ赋予新的值,因为这样在后面的计算中会对预测值产生影响。
现在我们来说一下导数前面的那个α。这叫学习率(learning rate),也叫梯度下降的步长(stride)。想象一下如果我们知道要往前走,虽然不知道我们的重点在多远,但是也不至于1厘米1厘米的往前蹭吧?这也太谨慎了。当然也不能劈着叉往前走,这也太没心没肺了。那么我们用什么步长往前走又能尽快到达重点又不至于越过终点呢?这就是要控制这个学习率,如果太低,那么计算重复量大,影响效率;如果太高,然后会到了最低点以后还继续走,可能走到比初始值还高的地方。
一般来讲学习率的的选择在 [0.0001, 0.001, 0.01, 0.1, 1] 之间,这是个超参数(hyperparameter),需要在建模的时候调参(hyperparameter selection)。
梯度下降大家族 如果你认为梯度下降就这一种方法你就太naive了,科学家总能给我们增加学习任务,下面来介绍一下都有哪些梯度下降法:
(1)批量梯度下降(Batch Gradient Descent)
这是一种最最常见的形式,也就是把所有的样本都用来参加更新参数θ。也就是我们之前讨论的梯度下降,公式是一样的,这里m就是代表需要所有样本的参与:
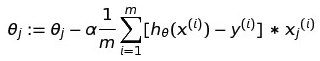
(2)随机梯度下降(Stochastic Gradient Descent)
这种梯度下降是随机的挑选一个样本进行下降算法,而不是批量的m个,对应的公式是这样:
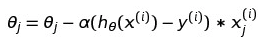
(3)小批量梯度下降(Mini-batch Gradient Descent)
小批量是随机和批量的中间值,这个值你可以随便来选,也就是把批量的m替换成来你希望的n个即可,这个n一般会选择2的多少次方个样本。
