宏观理解
线性回归就是在所有数据点中用最小二乘估计拟合出来一条直线,比如一个二维空间中,已知房屋面积,预测房屋价值。这时候就可以寻找一种面积和房价的线性关系,这样将来给出面积之后,自然就可以对应给出相应的房价。比如下图所示,x轴对应房屋面积,y轴对应价格,线性回归要做的就是拟合出一条粉色的线,使得所有点到这条线的距离加和最小:
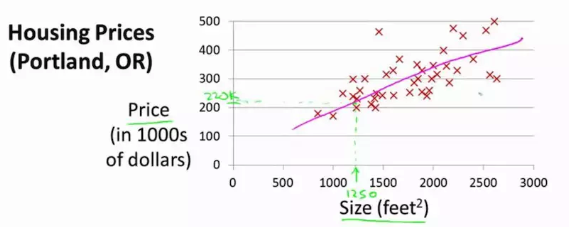
微观分析
上面所说的一种线性关系,用数学公式表达就是:
就是对应的输出预测结果房屋价格,x就是输入变量面积,那么模型所学习得到的就是θ0和θ1,其中θ0是截距。
这是最简单的形式,当然如果有很多的特征向量,公式就变成了:
。其中x0默认为是1,所以在之前的公式中我就省略了。
现在我们深入挖掘一下线性回归模型这个黑盒子里面做了什么事情
我们把换成另外一种写法
,在这里我们管hθ(x)叫hypothsis。可以想像成hθ(x)就是有特征向量和模型参数共同参加的一个函数,无论这个函数里面是什么怎么构成组合的,我们都可以用hθ(x)来表示这个函数,既然它与y_hat相等,那么我们也可以写成y_hat = hθ(x)。为了简便,因为在多维数据里θ和x都是向量,所以我们通常写成向量化表示
。T是转置transpose,因为是向量乘法,所以需要转置才能和X相乘。
现在我们要做的就是让模型慢慢的学习这个θ变量了。这里我们用的是一种叫梯度下降的方法,概括的说,梯度下降的过程就是从一开始随机初始化所有θ一个值,然后通过观察当θ的值是这些的时候,预测出来的结果离真实结果还有多大差距。当然了我们希望差距越小越好,所以我们要循环的更新这个θ,直到和真实值足够近似,注意我说的“足够”并不是越相近越好,因为这又引出了一个过拟合(overfitting)的问题,即由于过度的与训练集相似,导致泛化能力差,在测试集上表现不好。
那么我们就有了两个问题:1. 怎么知道预测值与真实值有多大差距?2. 知道差距了以后怎么更新我们的参数θ呢?
对于第一个问题就需要以前提到过的代价函数(cost function)了。在这个模型,我们使用MSE(mean square error),通常我们用字母J来表示代价函数,所以我们有了如下公式(其中m是训练集中的instance个数):
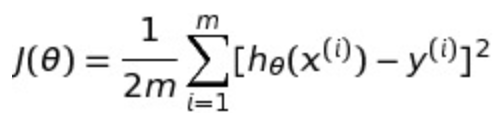
简单说就是把预测的y值与真实的y值相减,然后平方,这样就去掉了怎么是负数的情况,然后最外面套一个sum,就是所有数据点预测值与真实值差的平方的加和,最后再取mean。在取mean的时候分母中的2是因为在求导的时候会和后面的平方抵消,所以为了求导方便我们加了一个2,并不影响对比结果。
第一个问题我们已经解决了,得到了预测值和真实值之间的差距。那么现在我们解决第二个问题,怎么更新β使得这个损失函数最小?
我们需要梯度下降来完成这个任务。梯度下降做的就是一点一点的改变θ直到损失函数最小化。先放公式再解释:
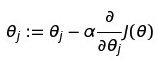
其中减去的值就是我们对于损失函数的求导,然后让原始的每个θ值都减去对应的导数值,循环一次完成后也就完成了一次梯度下降。直到收敛为止,也就到达了损失函数的最低点。其中导数前面的α是学习率(learning rate),这个是一个超参数用来决定下降的速度,如果设置的很小,那么下降的速度就会相对较慢,但是如果设置的太大了,就会起到反效果,反而不会收敛。把这个过程可视化出来就如下图。其中初始值就是我们一开始随机的θ,然后每次求出的导数,就是θ的下降方向,然后慢慢的直到θ达到最低点。(图中的w就是我们的θ)
现在我们也完成了第二个问题。线性回归的黑盒子大概就是这个过程了。
